The data consist of b-blocks mutually independent k-variate random variables Xij, i=1,..,b; j=1,..k. The random variable X is in block i and is associated with treatment j. It makes the multiple comparison of the Friedman test with or without ties. A first result is obtained by friedman.test of R.
friedman( judge, trt, evaluation, alpha = 0.05, group = TRUE, main = NULL, console = FALSE )
Arguments
| judge | Identification of the judge in the evaluation |
|---|---|
| trt | Treatment |
| evaluation | Variable |
| alpha | Significant test |
| group | TRUE or FALSE |
| main | Title |
| console | logical, print output |
Value
Statistics of the model
Design parameters
Statistical summary of the study variable
Comparison between treatments
Formation of treatment groups
Details
The post hoc friedman test is using the criterium Fisher's least significant difference (LSD)
References
Practical Nonparametrics Statistics. W.J. Conover, 1999
See also
BIB.test, DAU.test,
duncan.test, durbin.test,
HSD.test, kruskal, LSD.test,
Median.test, PBIB.test, REGW.test,
scheffe.test, SNK.test,
waerden.test, waller.test,
plot.group
Examples
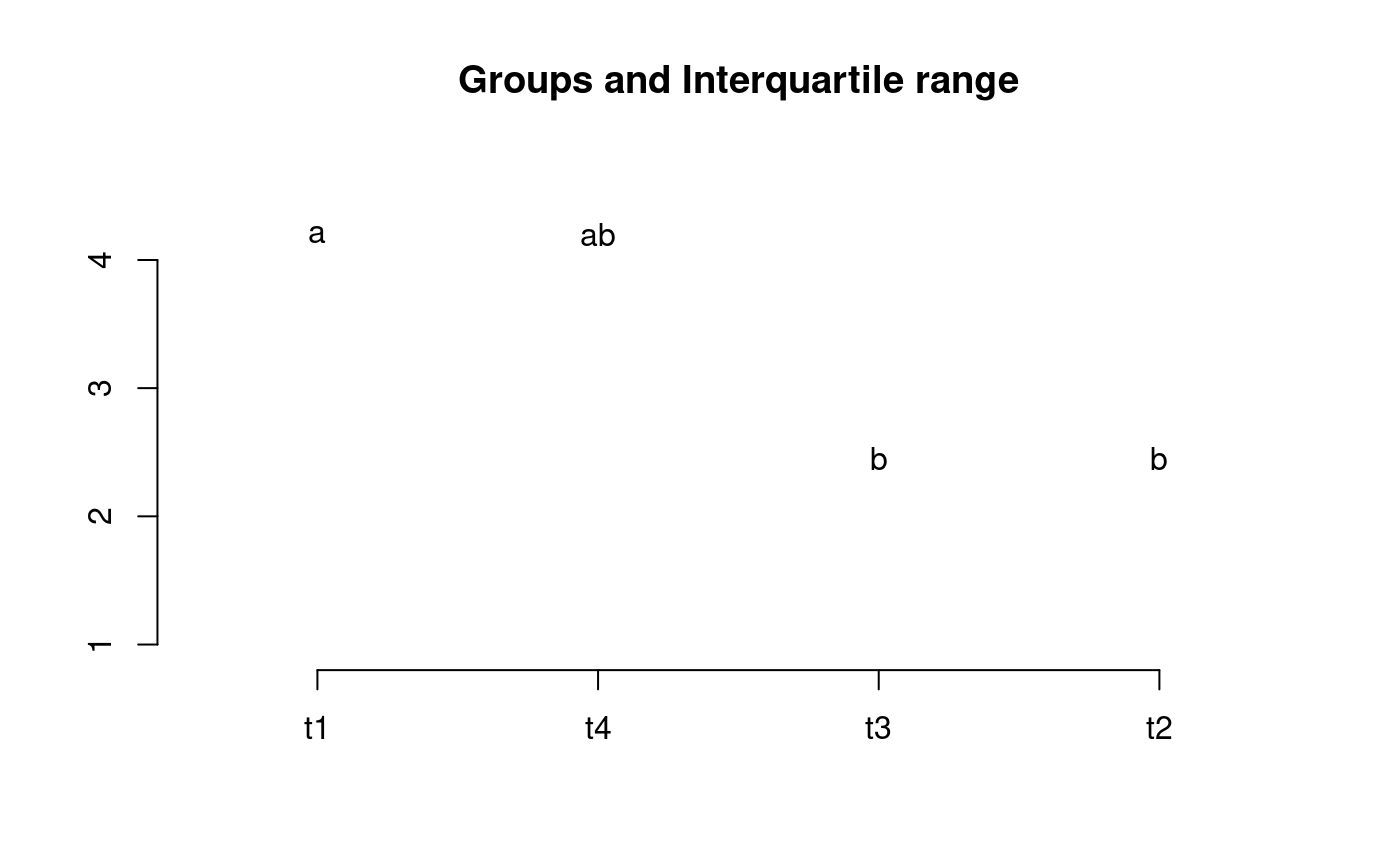
library(agricolae) data(grass) out<-with(grass,friedman(judge,trt, evaluation,alpha=0.05, group=TRUE,console=TRUE, main="Data of the book of Conover"))#> #> Study: Data of the book of Conover #> #> trt, Sum of the ranks #> #> evaluation r #> t1 38.0 12 #> t2 23.5 12 #> t3 24.5 12 #> t4 34.0 12 #> #> Friedman's Test #> =============== #> Adjusted for ties #> Critical Value: 8.097345 #> P.Value Chisq: 0.04404214 #> F Value: 3.192198 #> P.Value F: 0.03621547 #> #> Post Hoc Analysis #> #> Alpha: 0.05 ; DF Error: 33 #> t-Student: 2.034515 #> LSD: 11.48168 #> #> Treatments with the same letter are not significantly different. #> #> Sum of ranks groups #> t1 38.0 a #> t4 34.0 ab #> t3 24.5 b #> t2 23.5 b#> Warning: NAs introduced by coercion#endgraph