On the usage of the pbkrtest package

Søren Højsgaard1 and Ulrich Halekoh2

2020-02-20

Source: vignettes/Intro_pbkrtest.Rmd

  1. Head of Department of Mathematical Sciences and Associate Professor of statistics at Aalborg University ().

  1. Associate Professor, Department of Public Health, University of Southern Denmark, Denmark ().

Introduction

The data is a list of two vectors, giving the wear of shoes of materials A and B for one foot each of ten boys.

data(shoes, package="MASS")
shoes
$A
 [1] 13.2  8.2 10.9 14.3 10.7  6.6  9.5 10.8  8.8 13.3

$B
 [1] 14.0  8.8 11.2 14.2 11.8  6.4  9.8 11.3  9.3 13.6

A plot clearly reveals that boys wear their shoes differently.

plot(A~1, data=shoes, col="red",lwd=2, pch=1, ylab="wear", xlab="boy")
points(B~1, data=shoes, col="blue", lwd=2, pch=2)
points(I((A+B)/2)~1, data=shoes, pch="-", lwd=2)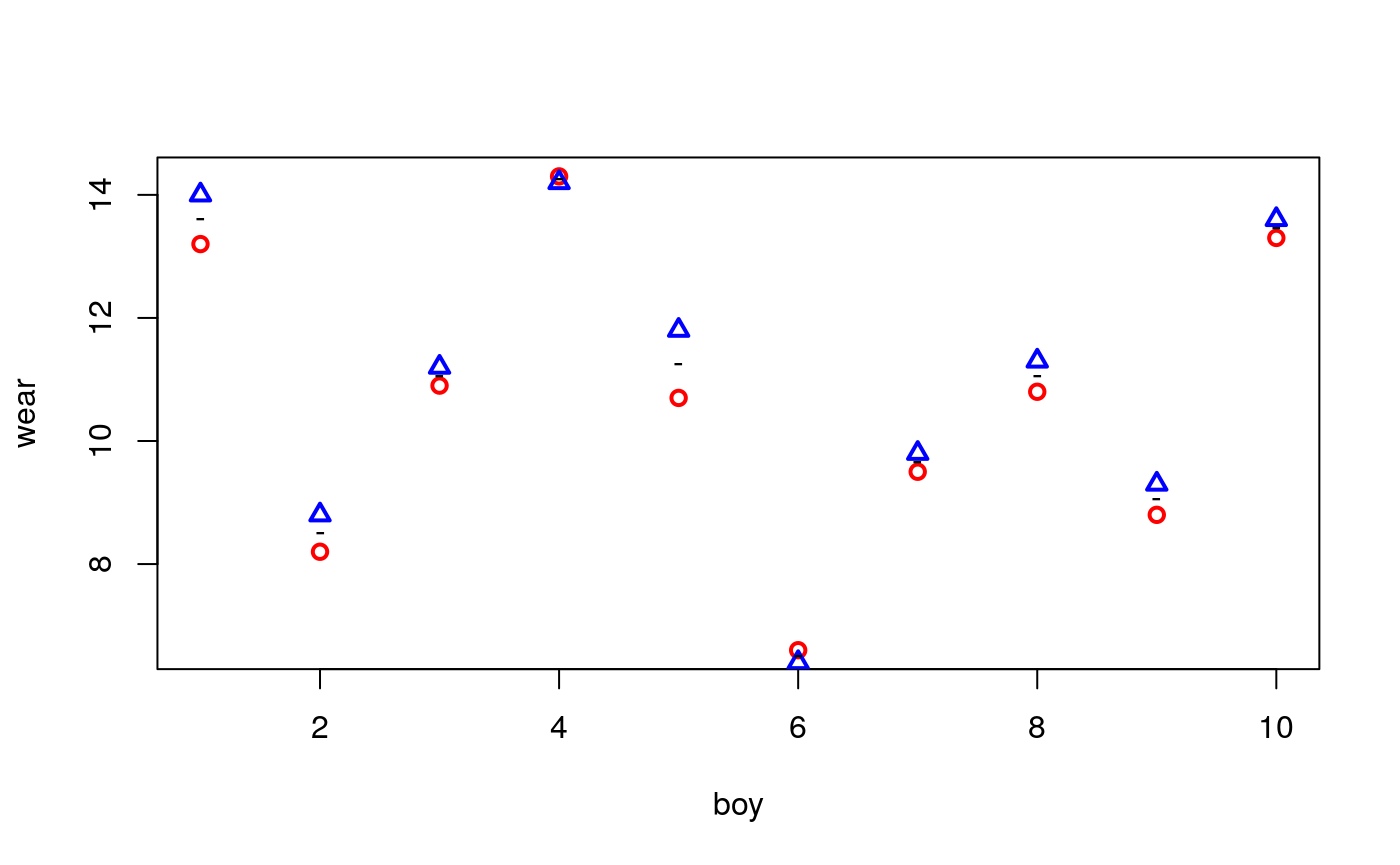

One option for testing the effect of materials is to make a paired \(t\)–test. The following forms are equivalent:

r1<-t.test(shoes$A, shoes$B, paired=T)
r2<-t.test(shoes$A-shoes$B)
r1

    Paired t-test

data:  shoes$A and shoes$B
t = -3.3489, df = 9, p-value = 0.008539
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.6869539 -0.1330461
sample estimates:
mean of the differences 
                  -0.41

To work with data in a mixed model setting we create a dataframe, and for later use we also create an imbalanced version of data:

boy <- rep(1:10,2)
boyf<- factor(letters[boy])
mat <- factor(c(rep("A", 10), rep("B",10)))
## Balanced data:
shoe.b <- data.frame(wear=unlist(shoes), boy=boy, boyf=boyf, mat=mat)
head(shoe.b)
   wear boy boyf mat
A1 13.2   1    a   A
A2  8.2   2    b   A
A3 10.9   3    c   A
A4 14.3   4    d   A
A5 10.7   5    e   A
A6  6.6   6    f   A
## Imbalanced data; delete (boy=1, mat=1) and (boy=2, mat=b)
shoe.i <-  shoe.b[-c(1,12),]

We fit models to the two datasets:

lmm1.b  <- lmer( wear ~ mat + (1|boyf), data=shoe.b )
lmm0.b  <- update( lmm1.b, .~. - mat)
lmm1.i  <- lmer( wear ~ mat + (1|boyf), data=shoe.i )
lmm0.i  <- update(lmm1.i, .~. - mat)

The asymptotic likelihood ratio test shows stronger significance than the \(t\)–test:

anova( lmm1.b, lmm0.b, test="Chisq" ) ## Balanced data
refitting model(s) with ML (instead of REML)
Data: shoe.b
Models:
lmm0.b: wear ~ (1 | boyf)
lmm1.b: wear ~ mat + (1 | boyf)
       Df    AIC    BIC  logLik deviance Chisq Chi Df Pr(>Chisq)   
lmm0.b  3 67.909 70.896 -30.955   61.909                           
lmm1.b  4 61.817 65.800 -26.909   53.817 8.092      1   0.004446 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova( lmm1.i, lmm0.i, test="Chisq" ) ## Imbalanced data
refitting model(s) with ML (instead of REML)
Data: shoe.i
Models:
lmm0.i: wear ~ (1 | boyf)
lmm1.i: wear ~ mat + (1 | boyf)
       Df    AIC    BIC  logLik deviance Chisq Chi Df Pr(>Chisq)  
lmm0.i  3 63.869 66.540 -28.934   57.869                          
lmm1.i  4 60.777 64.339 -26.389   52.777 5.092      1    0.02404 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Kenward–Roger approach

The Kenward–Roger approximation is exact for the balanced data in the sense that it produces the same result as the paired \(t\)–test.

( kr.b<-KRmodcomp(lmm1.b, lmm0.b) )
F-test with Kenward-Roger approximation; time: 0.11 sec
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
        stat    ndf    ddf F.scaling  p.value   
Ftest 11.215  1.000  9.000         1 0.008539 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(kr.b)
F-test with Kenward-Roger approximation; time: 0.11 sec
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
         stat    ndf    ddf F.scaling  p.value   
Ftest  11.215  1.000  9.000         1 0.008539 **
FtestU 11.215  1.000  9.000           0.008539 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Relevant information can be retrieved with

getKR(kr.b, "ddf")
[1] 9

For the imbalanced data we get

(kr.i<-KRmodcomp(lmm1.i, lmm0.i))
F-test with Kenward-Roger approximation; time: 0.03 sec
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
        stat    ndf    ddf F.scaling p.value  
Ftest 5.9893 1.0000 7.0219         1 0.04418 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Notice that this result is similar to but not identical to the paired \(t\)–test when the two relevant boys are removed:

shoes2 <- list(A=shoes$A[-(1:2)], B=shoes$B[-(1:2)])
t.test(shoes2$A, shoes2$B, paired=T)

    Paired t-test

data:  shoes2$A and shoes2$B
t = -2.3878, df = 7, p-value = 0.04832
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.671721705 -0.003278295
sample estimates:
mean of the differences 
                -0.3375

Parametric bootstrap

Parametric bootstrap provides an alternative but many simulations are often needed to provide credible results (also many more than shown here; in this connection it can be useful to exploit that computings can be made en parallel, see the documentation):

(pb.b <- PBmodcomp(lmm1.b, lmm0.b, nsim=500, cl=2) )
Bootstrap test; time: 4.20 sec;samples: 500; extremes: 3;
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
         stat df  p.value   
LRT    8.1197  1 0.004379 **
PBtest 8.1197    0.007984 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary( pb.b )
Bootstrap test; time: 4.20 sec;samples: 500; extremes: 3;
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
           stat     df    ddf  p.value   
LRT      8.1197 1.0000        0.004379 **
PBtest   8.1197               0.007984 **
Gamma    8.1197               0.009788 **
Bartlett 6.5439 1.0000        0.010524 * 
F        8.1197 1.0000 10.305 0.016785 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

For the imbalanced data, the result is similar to the result from the paired \(t\) test.

(pb.i<-PBmodcomp(lmm1.i, lmm0.i, nsim=500, cl=2))
Bootstrap test; time: 4.49 sec;samples: 500; extremes: 28;
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
         stat df p.value  
LRT    5.1151  1 0.02372 *
PBtest 5.1151    0.05788 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(pb.i)
Bootstrap test; time: 4.49 sec;samples: 500; extremes: 28;
large : wear ~ mat + (1 | boyf)
small : wear ~ (1 | boyf)
           stat     df    ddf p.value  
LRT      5.1151 1.0000        0.02372 *
PBtest   5.1151               0.05788 .
Gamma    5.1151               0.04964 *
Bartlett 3.9029 1.0000        0.04820 *
F        5.1151 1.0000 8.4391 0.05192 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Matrices for random effects

The matrices involved in the random effects can be obtained with

shoe3 <- subset(shoe.b, boy<=5)
shoe3 <- shoe3[order(shoe3$boy), ]
lmm1  <- lmer( wear ~ mat + (1|boyf), data=shoe3 )
str( SG <- get_SigmaG( lmm1 ), max=2)
List of 3
 $ Sigma   :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
 $ G       :List of 2
  ..$ :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
  ..$ :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
 $ n.ggamma: int 2
round( SG$Sigma*10 )
10 x 10 sparse Matrix of class "dgCMatrix"
   [[ suppressing 10 column names 'A1', 'B1', 'A2' ... ]]
                                
A1 53 52  .  .  .  .  .  .  .  .
B1 52 53  .  .  .  .  .  .  .  .
A2  .  . 53 52  .  .  .  .  .  .
B2  .  . 52 53  .  .  .  .  .  .
A3  .  .  .  . 53 52  .  .  .  .
B3  .  .  .  . 52 53  .  .  .  .
A4  .  .  .  .  .  . 53 52  .  .
B4  .  .  .  .  .  . 52 53  .  .
A5  .  .  .  .  .  .  .  . 53 52
B5  .  .  .  .  .  .  .  . 52 53
SG$G
[[1]]
10 x 10 sparse Matrix of class "dgCMatrix"
   [[ suppressing 10 column names 'A1', 'B1', 'A2' ... ]]
                      
A1 1 1 . . . . . . . .
B1 1 1 . . . . . . . .
A2 . . 1 1 . . . . . .
B2 . . 1 1 . . . . . .
A3 . . . . 1 1 . . . .
B3 . . . . 1 1 . . . .
A4 . . . . . . 1 1 . .
B4 . . . . . . 1 1 . .
A5 . . . . . . . . 1 1
B5 . . . . . . . . 1 1

[[2]]
10 x 10 sparse Matrix of class "dgCMatrix"
                         
 [1,] 1 . . . . . . . . .
 [2,] . 1 . . . . . . . .
 [3,] . . 1 . . . . . . .
 [4,] . . . 1 . . . . . .
 [5,] . . . . 1 . . . . .
 [6,] . . . . . 1 . . . .
 [7,] . . . . . . 1 . . .
 [8,] . . . . . . . 1 . .
 [9,] . . . . . . . . 1 .
[10,] . . . . . . . . . 1