An introduction to R for Agricultural Research

Blogs

9 May 2018

Introduction

R is a free, open-source programming language and software environment for statistical computing, bioinformatics, visualization and general computing. R provides a wide variety of statistical and graphical techniques, and is highly extensible. The latest version of R is 3.5.0 which can be obtained from https://cran.r-project.org/bin/windows/base/.

R R-3.5.0 for Windows (32/64 bit)

RStudio RStudio

Manual An Introduction to R

Ref Card R Reference Card

New York Times New York Times

Nature Article Nature Article

Regression Analysis

Quantifying dependency of a normal response on quantitative explanatory variable(s)

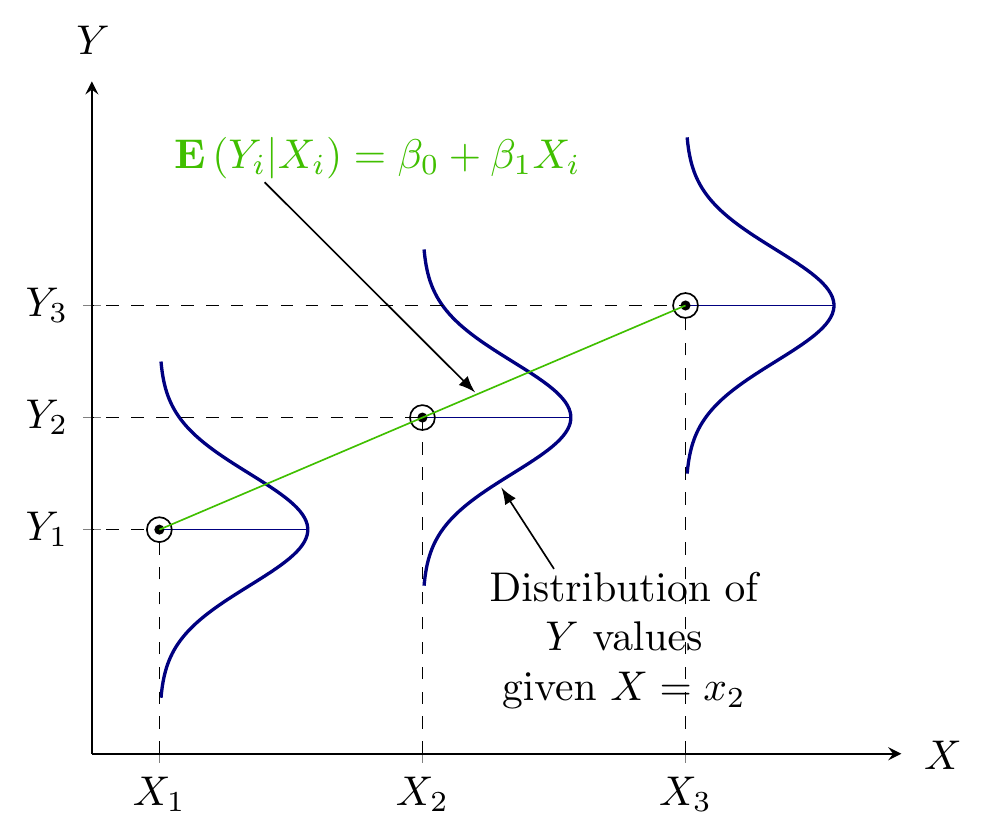
Figure 1: Population Regression Function

Simple Linear Regression

Quantifying dependency of a normal response on a quantitative explanatory variable

Example

Fertilizer (Kg/acre)	Production (Bushels/acre)
100	70
200	70
400	80
500	100

# Fertilizer (Kg/acre)
# Production (Bushels/acre)
Fertilizer <- c(100, 200, 400, 500)
Production <- c( 70,  70,  80, 100)
df1        <- data.frame(Fertilizer, Production)
df1

  Fertilizer Production
1        100         70
2        200         70
3        400         80
4        500        100

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p1 <- 
  ggplot(data = df1, mapping = aes(x = Fertilizer, y = Production)) + 
  geom_point() +
  labs(x = "Fertilizer", y = "Production") +
  theme_bw()
print(p1)

fm1 <- lm(formula = Production ~ Fertilizer, data = df1)
summary(fm1)


Call:
lm(formula = Production ~ Fertilizer, data = df1)

Residuals:
 1  2  3  4 
 4 -3 -7  6 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 59.00000    7.95299   7.419   0.0177 *
Fertilizer   0.07000    0.02345   2.985   0.0963 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.416 on 2 degrees of freedom
Multiple R-squared:  0.8167,    Adjusted R-squared:  0.725 
F-statistic: 8.909 on 1 and 2 DF,  p-value: 0.0963

anova(fm1)

Analysis of Variance Table

Response: Production
           Df Sum Sq Mean Sq F value Pr(>F)  
Fertilizer  1    490     490  8.9091 0.0963 .
Residuals   2    110      55                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Example

Fertilizer	Yield
0.3	10
0.6	15
0.9	30
1.2	35
1.5	25
1.8	30
2.1	50
2.4	45

Fert  <- c(0.3, 0.6, 0.9, 1.2, 1.5, 1.8, 2.1, 2.4)
Yield <- c(10, 15, 30, 35, 25, 30, 50, 45)
df2   <- data.frame(Fert, Yield)
df2

  Fert Yield
1  0.3    10
2  0.6    15
3  0.9    30
4  1.2    35
5  1.5    25
6  1.8    30
7  2.1    50
8  2.4    45

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p2 <- 
  ggplot(data = df2, mapping = aes(x = Fert, y = Yield)) + 
  geom_point() +
  labs(x = "Fertilizer", y = "Yield") +
  theme_bw()
print(p2)

fm2 <- lm(formula = Yield ~ Fert, data = df2)
summary(fm2)


Call:
lm(formula = Yield ~ Fert, data = df2)

Residuals:
   Min     1Q Median     3Q    Max 
-7.441 -4.018 -2.441  7.351  7.798 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)    8.036      5.504   1.460   0.1946   
Fert          16.270      3.633   4.478   0.0042 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.064 on 6 degrees of freedom
Multiple R-squared:  0.7697,    Adjusted R-squared:  0.7313 
F-statistic: 20.05 on 1 and 6 DF,  p-value: 0.004202

anova(fm2)

Analysis of Variance Table

Response: Yield
          Df Sum Sq Mean Sq F value   Pr(>F)   
Fert       1 1000.6  1000.6  20.052 0.004202 **
Residuals  6  299.4    49.9                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Example

Weekly Income ($)	Weekly Expenditures ($)
80	70
100	65
120	90
140	95
160	110
180	115
200	120
220	140
240	155
260	150

# Weekly Income ($) of a Family
# Weekly Expenditures ($) of a Family
Income       <- seq(from = 80, to = 260, by = 20)
Expenditures <- c(70, 65, 90, 95, 110, 115, 120, 140, 155, 150)
df3          <- data.frame(Income, Expenditures)
df3

   Income Expenditures
1      80           70
2     100           65
3     120           90
4     140           95
5     160          110
6     180          115
7     200          120
8     220          140
9     240          155
10    260          150

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p3 <- 
  ggplot(data = df3, mapping = aes(x = Income, y = Expenditures)) + 
  geom_point() +
  scale_x_continuous(labels = scales::dollar) +
  scale_y_continuous(labels = scales::dollar) +
  labs(x = "Weekly income, $", y = "Weekly consumption expenditures, $") +
  theme_bw()
print(p3)

fm3 <- lm(formula = Expenditures ~ Income, data = df3)
summary(fm3)


Call:
lm(formula = Expenditures ~ Income, data = df3)

Residuals:
    Min      1Q  Median      3Q     Max 
-10.364  -4.977   1.409   4.364   8.364 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 24.45455    6.41382   3.813  0.00514 ** 
Income       0.50909    0.03574  14.243 5.75e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.493 on 8 degrees of freedom
Multiple R-squared:  0.9621,    Adjusted R-squared:  0.9573 
F-statistic: 202.9 on 1 and 8 DF,  p-value: 5.753e-07

anova(fm3)

Analysis of Variance Table

Response: Expenditures
          Df Sum Sq Mean Sq F value    Pr(>F)    
Income     1 8552.7  8552.7  202.87 5.753e-07 ***
Residuals  8  337.3    42.2                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Multiple Linear Regression

Quantifying dependency of a normal response on two or more quantitative explanatory variables

Example

Fertilizer (Kg)	Rainfall (mm)	Yield (Kg)
100	10	40
200	20	50
300	10	50
400	30	70
500	20	65
600	20	65
700	30	80

# Fertilizer (Kg)
# Rainfall (mm)
# Yield (Kg)
Fertilizer <- seq(from = 100, to = 700, by = 100)
Rainfall   <- c(10, 20, 10, 30, 20, 20, 30)
Yield      <- c(40, 50, 50, 70, 65, 65, 80)
df4        <- data.frame(Fertilizer, Rainfall, Yield)
df4

  Fertilizer Rainfall Yield
1        100       10    40
2        200       20    50
3        300       10    50
4        400       30    70
5        500       20    65
6        600       20    65
7        700       30    80

library(car)
# if (!require("car")) install.packages("car")
car::scatter3d(formula = Yield ~ Fertilizer + Rainfall, data = df4)

fm4 <- lm(formula = Yield ~ Fertilizer + Rainfall, data = df4)
summary(fm4)


Call:
lm(formula = Yield ~ Fertilizer + Rainfall, data = df4)

Residuals:
      1       2       3       4       5       6       7 
-0.2381 -2.3810  2.1429  1.6667  1.1905 -2.6190  0.2381 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 28.095238   2.491482  11.277 0.000352 ***
Fertilizer   0.038095   0.005832   6.532 0.002838 ** 
Rainfall     0.833333   0.154303   5.401 0.005690 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.315 on 4 degrees of freedom
Multiple R-squared:  0.9814,    Adjusted R-squared:  0.972 
F-statistic: 105.3 on 2 and 4 DF,  p-value: 0.0003472

anova(fm4)

Analysis of Variance Table

Response: Yield
           Df Sum Sq Mean Sq F value    Pr(>F)    
Fertilizer  1 972.32  972.32 181.500 0.0001756 ***
Rainfall    1 156.25  156.25  29.167 0.0056899 ** 
Residuals   4  21.43    5.36                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

library(lm.beta)
# if (!require("lm.beta")) install.packages("lm.beta")
lm.beta(fm4)


Call:
lm(formula = Yield ~ Fertilizer + Rainfall, data = df4)

Standardized Coefficients::
(Intercept)  Fertilizer    Rainfall 
  0.0000000   0.5944301   0.4914732

Polynomial Regression Analysis

Quantifying non-linear dependency of a normal response on quantitative explanatory variable(s)

Example

An experiment was conducted to evaluate the effects of different levels of nitrogen. Three levels of nitrogen: 0, 10 and 20 grams per plot were used in the experiment. Each treatment was replicated twice and data is given below:

Nitrogen	Yield
0	5
0	7
10	15
10	17
20	9
20	11

Nitrogen <- c(0, 0, 10, 10, 20, 20)
Yield    <- c(5, 7, 15, 17,  9, 11)
df5      <- data.frame(Nitrogen, Yield)
df5

  Nitrogen Yield
1        0     5
2        0     7
3       10    15
4       10    17
5       20     9
6       20    11

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p5 <- 
  ggplot(data = df5, mapping = aes(x = Nitrogen, y = Yield)) + 
  geom_point() +
  labs(x = "Nitrogen", y = "Yield") +
  theme_bw()
print(p5)

fm5 <- lm(formula = Yield ~ Nitrogen + I(Nitrogen^2), data = df5)
# fm5 <- lm(formula = Yield ~ poly(x = Nitrogen, degree = 2, raw = TRUE), data = df5)
summary(fm5)


Call:
lm(formula = Yield ~ Nitrogen + I(Nitrogen^2), data = df5)

Residuals:
 1  2  3  4  5  6 
-1  1 -1  1 -1  1 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept)    6.00000    1.00000   6.000  0.00927 **
Nitrogen       1.80000    0.25495   7.060  0.00584 **
I(Nitrogen^2) -0.08000    0.01225  -6.532  0.00729 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.414 on 3 degrees of freedom
Multiple R-squared:  0.9441,    Adjusted R-squared:  0.9068 
F-statistic: 25.33 on 2 and 3 DF,  p-value: 0.01322

anova(fm5)

Analysis of Variance Table

Response: Yield
              Df Sum Sq Mean Sq F value   Pr(>F)   
Nitrogen       1 16.000  16.000   8.000 0.066276 . 
I(Nitrogen^2)  1 85.333  85.333  42.667 0.007292 **
Residuals      3  6.000   2.000                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Analysis of Variance (ANOVA)

Comparing means of Normal dependent variable for levels of different factor(s)

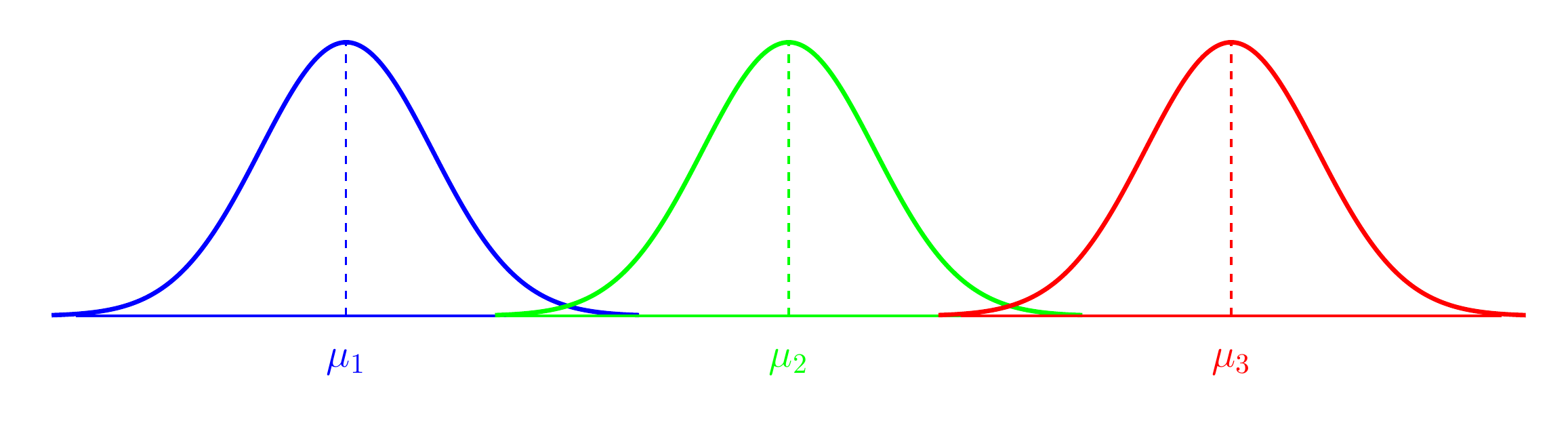
Figure 2: Analysis of Variance

Example

Yield	Variety
5	V1
6	V1
7	V1
15	V2
16	V2
17	V2

Yield   <- c(5, 6, 7, 15, 16, 17)
Variety <- gl(n = 2, k = 3, length = 2*3, labels = c("V1", "V2"))
df6     <- data.frame(Yield, Variety)
df6

  Yield Variety
1     5      V1
2     6      V1
3     7      V1
4    15      V2
5    16      V2
6    17      V2

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p6 <- 
  ggplot(data = df6, mapping = aes(x = Variety, y = Yield)) + 
  geom_point() +
  geom_boxplot() +
  labs(x = "Variety", y = "Yield") +
  theme_bw()
print(p6)

fm6 <- lm(formula = Yield ~ Variety, data = df6)
summary(fm6)


Call:
lm(formula = Yield ~ Variety, data = df6)

Residuals:
         1          2          3          4          5          6 
-1.000e+00 -4.774e-15  1.000e+00 -1.000e+00 -1.110e-16  1.000e+00 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.0000     0.5774   10.39 0.000484 ***
VarietyV2    10.0000     0.8165   12.25 0.000255 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1 on 4 degrees of freedom
Multiple R-squared:  0.974, Adjusted R-squared:  0.9675 
F-statistic:   150 on 1 and 4 DF,  p-value: 0.0002552

anova(fm6)

Analysis of Variance Table

Response: Yield
          Df Sum Sq Mean Sq F value    Pr(>F)    
Variety    1    150     150     150 0.0002552 ***
Residuals  4      4       1                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Example

Yield	Variety
5	V1
7	V1
15	V2
17	V2
17	V3
19	V3

Yield   <- c(5, 7, 15, 17, 17, 19)
Variety <- gl(n = 3, k = 2, length = 3*2, labels = c("V1", "V2", "V3"))
df7     <- data.frame(Yield, Variety)
df7

  Yield Variety
1     5      V1
2     7      V1
3    15      V2
4    17      V2
5    17      V3
6    19      V3

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p7 <- 
  ggplot(data = df7, mapping = aes(x = Variety, y = Yield)) + 
  geom_point() +
  geom_boxplot() +
  labs(x = "Variety", y = "Yield") +
  theme_bw()
print(p7)

fm7 <- lm(formula = Yield ~ Variety, data = df7)
summary(fm7)


Call:
lm(formula = Yield ~ Variety, data = df7)

Residuals:
 1  2  3  4  5  6 
-1  1 -1  1 -1  1 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)    6.000      1.000   6.000  0.00927 **
VarietyV2     10.000      1.414   7.071  0.00582 **
VarietyV3     12.000      1.414   8.485  0.00344 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.414 on 3 degrees of freedom
Multiple R-squared:  0.965, Adjusted R-squared:  0.9416 
F-statistic: 41.33 on 2 and 3 DF,  p-value: 0.006553

anova(fm7)

Analysis of Variance Table

Response: Yield
          Df Sum Sq Mean Sq F value   Pr(>F)   
Variety    2 165.33  82.667  41.333 0.006553 **
Residuals  3   6.00   2.000                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Analysis of Covariance (ANCOVA)

Quantifying dependency of a normal response on quantitative explanatory variable(s)

Comparing means of Normal dependent variable for levels of different factor(s)

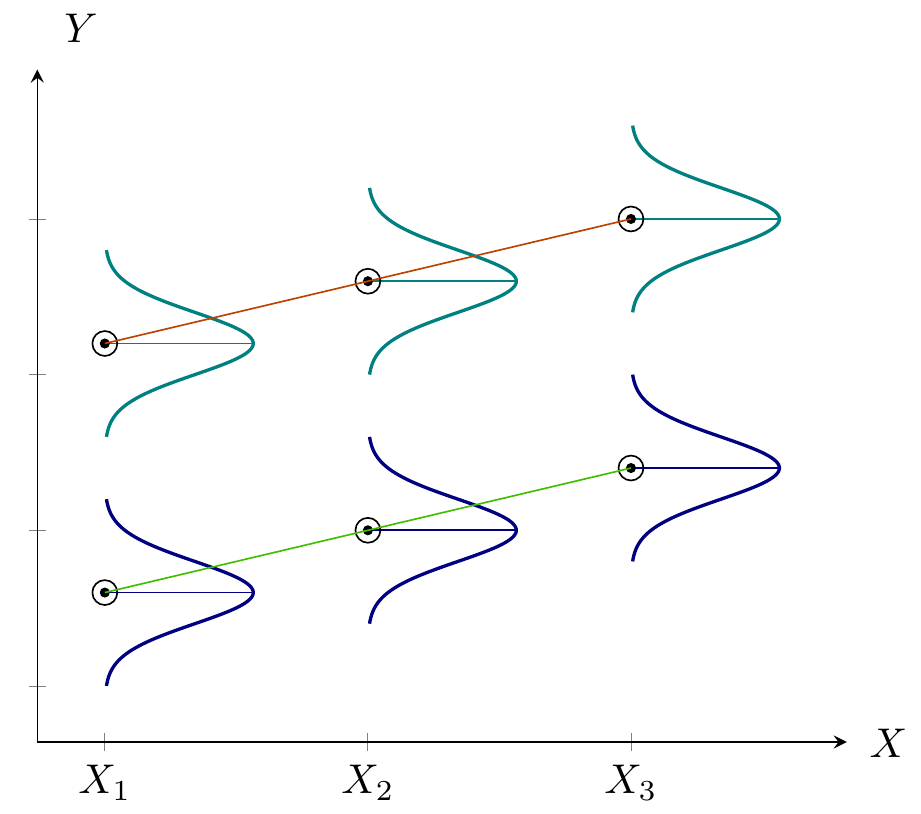
Figure 3: Analysis of Covariance

Example

Yield	Fert	Variety
51	80	V1
52	80	V1
53	90	V1
54	90	V1
56	100	V1
57	100	V1
55	80	V2
56	80	V2
58	90	V2
59	90	V2
62	100	V2
63	100	V2

Yield    <- c(51, 52, 53, 54, 56, 57, 55, 56, 58, 59, 62, 63)
Fert     <- rep(x = c(80, 90, 100), each = 2)
Variety  <- gl(n = 2, k = 6, length = 2*6, labels = c("V1", "V2"), ordered = FALSE)
df8         <- data.frame(Yield, Fert, Variety)
df8

   Yield Fert Variety
1     51   80      V1
2     52   80      V1
3     53   90      V1
4     54   90      V1
5     56  100      V1
6     57  100      V1
7     55   80      V2
8     56   80      V2
9     58   90      V2
10    59   90      V2
11    62  100      V2
12    63  100      V2

Same intercepts but different slopes

fm8 <- lm(formula = Yield ~ Fert + Variety, data = df8)
summary(fm8)


Call:
lm(formula = Yield ~ Fert + Variety, data = df8)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.8333 -0.8333  0.1667  0.1667  1.1667 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 26.83333    2.54557   10.54 2.30e-06 ***
Fert         0.30000    0.02805   10.69 2.04e-06 ***
VarietyV2    5.00000    0.45812   10.91 1.72e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7935 on 9 degrees of freedom
Multiple R-squared:  0.9629,    Adjusted R-squared:  0.9546 
F-statistic: 116.7 on 2 and 9 DF,  p-value: 3.657e-07

anova(fm8)

Analysis of Variance Table

Response: Yield
          Df Sum Sq Mean Sq F value    Pr(>F)    
Fert       1 72.000   72.00  114.35 2.042e-06 ***
Variety    1 75.000   75.00  119.12 1.720e-06 ***
Residuals  9  5.667    0.63                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p8 <- 
  ggplot(data = df8, mapping = aes(x = Fert, y = Yield, color = Variety)) + 
  geom_point() +
  geom_line(mapping = aes(y = predict(fm8))) +
  labs(x = "Fert", y = "Yield") +
  theme_bw()
print(p8)

Different intercepts and different slopes

fm9 <- lm(formula = Yield ~ Fert * Variety, data = df8)
summary(fm9)


Call:
lm(formula = Yield ~ Fert * Variety, data = df8)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.83333 -0.33333 -0.08333  0.66667  0.66667 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    31.33333    3.05903  10.243 7.09e-06 ***
Fert            0.25000    0.03385   7.385 7.73e-05 ***
VarietyV2      -4.00000    4.32612  -0.925   0.3822    
Fert:VarietyV2  0.10000    0.04787   2.089   0.0701 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.677 on 8 degrees of freedom
Multiple R-squared:  0.976, Adjusted R-squared:  0.967 
F-statistic: 108.4 on 3 and 8 DF,  p-value: 8.11e-07

anova(fm9)

Analysis of Variance Table

Response: Yield
             Df Sum Sq Mean Sq  F value    Pr(>F)    
Fert          1 72.000  72.000 157.0909 1.538e-06 ***
Variety       1 75.000  75.000 163.6364 1.315e-06 ***
Fert:Variety  1  2.000   2.000   4.3636   0.07013 .  
Residuals     8  3.667   0.458                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p9 <- 
  ggplot(data = df8, mapping = aes(x = Fert, y = Yield, color = Variety)) + 
  geom_point() +
  geom_line(mapping = aes(y = predict(fm9))) +
  labs(x = "Fert", y = "Yield") +
  theme_bw()
print(p9)

Correlation Analysis

Linear Relationship between Quantitative Variables

Simple Correlation Analysis

Linear Relationship between Two Quantitative Variables

$\left(X_{1},X_{2}\right)$

Example

Sparrow Wing length (cm)	Sparrow Tail length (cm)
10.4	7.4
10.8	7.6
11.1	7.9
10.2	7.2
10.3	7.4
10.2	7.1
10.7	7.4
10.5	7.2
10.8	7.8
11.2	7.7
10.6	7.8
11.4	8.3

WingLength  <- c(10.4, 10.8, 11.1, 10.2, 10.3, 10.2, 10.7, 10.5, 10.8, 11.2, 10.6, 11.4)
TailLength  <- c(7.4, 7.6, 7.9, 7.2, 7.4, 7.1, 7.4, 7.2, 7.8, 7.7, 7.8, 8.3)
df10        <- data.frame(WingLength, TailLength)
df10

   WingLength TailLength
1        10.4        7.4
2        10.8        7.6
3        11.1        7.9
4        10.2        7.2
5        10.3        7.4
6        10.2        7.1
7        10.7        7.4
8        10.5        7.2
9        10.8        7.8
10       11.2        7.7
11       10.6        7.8
12       11.4        8.3

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p10 <- 
  ggplot(data = df10, mapping = aes(x= WingLength, y = TailLength)) + 
  geom_point() +
  labs(x = "Sparrow Wing Length (cm)", y = "Sparrow Tail Length (cm)") +
  theme_bw()
print(p10)

cor(df10$WingLength, df10$TailLength)

[1] 0.8703546

cor.test(df10$WingLength, df10$TailLength)


    Pearson's product-moment correlation

data:  df10$WingLength and df10$TailLength
t = 5.5893, df = 10, p-value = 0.0002311
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.5923111 0.9631599
sample estimates:
      cor 
0.8703546

Partial Correlation Analysis

Linear Relationship between Quantitative Variables while holding/keeping all other constants

$\left(X_{1},X_{2}\right)|X_{3}$

Example

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

LeafArea    <- c(72, 174, 116, 78, 134, 95, 113, 98, 148, 42)
LeafMoist   <- c(75, 81, 83, 79, 81, 80, 81, 74, 78, 58)
TotShLength <- c(307, 529, 632, 527, 442, 525, 481, 710, 422, 345)
df11        <- data.frame(LeafArea, LeafMoist, TotShLength)
df11

   LeafArea LeafMoist TotShLength
1        72        75         307
2       174        81         529
3       116        83         632
4        78        79         527
5       134        81         442
6        95        80         525
7       113        81         481
8        98        74         710
9       148        78         422
10       42        58         345

library(ppcor)
# if (!require("ppcor")) install.packages("ppcor")
pcor(df11)

$estimate
                LeafArea LeafMoist  TotShLength
LeafArea     1.000000000 0.6509096 -0.007012236
LeafMoist    0.650909618 1.0000000  0.324334659
TotShLength -0.007012236 0.3243347  1.000000000

$p.value
              LeafArea  LeafMoist TotShLength
LeafArea    0.00000000 0.05760462   0.9857154
LeafMoist   0.05760462 0.00000000   0.3944839
TotShLength 0.98571537 0.39448385   0.0000000

$statistic
               LeafArea LeafMoist TotShLength
LeafArea     0.00000000  2.268502 -0.01855309
LeafMoist    2.26850175  0.000000  0.90714704
TotShLength -0.01855309  0.907147  0.00000000

$n
[1] 10

$gp
[1] 1

$method
[1] "pearson"

Multiple Correlation Analysis

Linear Relationship between a Quantitative Variable and set of other Quantitative Variables

$\left(X_{1},\left[X_{2},X_{3}\right]\right)$

Example

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

fm12 <- lm(formula = TotShLength ~ LeafArea + LeafMoist, data = df11)
sqrt(summary(fm12)$r.squared)

[1] 0.421277

Completely Randomized Design (CRD)

Used when experimental material is homogeneous

Example

The following table shows some of the results of an experiment on the effects of applications of sulphur in reducing scab disease of potatoes. The object in applying sulphur is to increase the acidity of the soil, since scab does not thrive in very acid soil. In addition to untreated plots which serve as a control, 3 amounts of dressing were compared—300, 600, and 900 lb. per acre. Both a fall and a spring application of each amount was tested, so that in all there were seven distinct treatments. The sulphur was spread by hand on the surface of the soil, and then diced into a depth of about 4 inches. The quantity to be analyzed is the “scab index”. That is roughly speaking, the percentage of the surface area of the potato that is infected with scab. It is obtained by examining 100 potatoes at random from each plot, grading each potato on a scale from 0 to 100% infected, and taking the average.

ScabIndex <-
      c(
        12, 10,  24, 29, 
        30, 18,  32, 26, 
         9,  9,  16,  4,
        30,  7,  21,  9,
        16, 10,  18, 18,
        18, 24,  12, 19,
        10,  4,   4,  5,
        17,  7,  16, 17
      )
Trt  <- factor(
          x = rep(x = 1:7, times = c(8, 4, 4, 4, 4, 4, 4))
        , labels = c("O", "F3", "S3", "F6", "S6", "F9", "S9")
        )

df13 <- data.frame(Trt, ScabIndex)
df13

   Trt ScabIndex
1    O        12
2    O        10
3    O        24
4    O        29
5    O        30
6    O        18
7    O        32
8    O        26
9   F3         9
10  F3         9
11  F3        16
12  F3         4
13  S3        30
14  S3         7
15  S3        21
16  S3         9
17  F6        16
18  F6        10
19  F6        18
20  F6        18
21  S6        18
22  S6        24
23  S6        12
24  S6        19
25  F9        10
26  F9         4
27  F9         4
28  F9         5
29  S9        17
30  S9         7
31  S9        16
32  S9        17

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p13 <- 
  ggplot(data = df13, mapping = aes(x = Trt, y = ScabIndex)) + 
  geom_point() +
  geom_boxplot() +
  labs(x = "Treatment", y = "Scab Index") +
  theme_bw()
print(p13)

fm13 <- lm(formula = ScabIndex ~ Trt, data = df13)
summary(fm13)


Call:
lm(formula = ScabIndex ~ Trt, data = df13)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.625  -4.844   0.625   3.594  13.250 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   22.625      2.369   9.549 8.08e-10 ***
TrtF3        -13.125      4.104  -3.198 0.003734 ** 
TrtS3         -5.875      4.104  -1.432 0.164666    
TrtF6         -7.125      4.104  -1.736 0.094858 .  
TrtS6         -4.375      4.104  -1.066 0.296601    
TrtF9        -16.875      4.104  -4.112 0.000372 ***
TrtS9         -8.375      4.104  -2.041 0.051977 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.702 on 25 degrees of freedom
Multiple R-squared:  0.4641,    Adjusted R-squared:  0.3355 
F-statistic: 3.608 on 6 and 25 DF,  p-value: 0.01026

anova(fm13)

Analysis of Variance Table

Response: ScabIndex
          Df  Sum Sq Mean Sq F value  Pr(>F)  
Trt        6  972.34 162.057  3.6081 0.01026 *
Residuals 25 1122.88  44.915                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Randomized Complete Block Design (RCBD)

Used when experimental material is heterogenous in one direction

Example

Yield : Yield of barley, SoilType : Soil Type, and Trt : 5 sources and a control

Yield <- c(
             32.1,  35.6,   41.9,   35.4
          ,  30.1,  31.5,   37.1,   30.8
          ,  25.4,  27.4,   33.8,   31.1
          ,  24.1,  33.0,   35.6,   31.4
          ,  26.1,  31.0,   33.8,   31.9
          ,  23.2,  24.8,   26.7,   26.7
          )
SoilType <- gl(n = 4, k = 6, length = 4*6
               , labels = c("I", "II", "III", "IV"), ordered = FALSE)
Trt      <- gl(n = 6, k = 1, length = 4*6
               , labels = c("(NH4)2SO4", "NH4NO3", "CO(NH2)2", "Ca(NO3)2", "NaNO3", "Control"), ordered = FALSE)

df14 <- data.frame(Yield, SoilType, Trt)
df14

   Yield SoilType       Trt
1   32.1        I (NH4)2SO4
2   35.6        I    NH4NO3
3   41.9        I  CO(NH2)2
4   35.4        I  Ca(NO3)2
5   30.1        I     NaNO3
6   31.5        I   Control
7   37.1       II (NH4)2SO4
8   30.8       II    NH4NO3
9   25.4       II  CO(NH2)2
10  27.4       II  Ca(NO3)2
11  33.8       II     NaNO3
12  31.1       II   Control
13  24.1      III (NH4)2SO4
14  33.0      III    NH4NO3
15  35.6      III  CO(NH2)2
16  31.4      III  Ca(NO3)2
17  26.1      III     NaNO3
18  31.0      III   Control
19  33.8       IV (NH4)2SO4
20  31.9       IV    NH4NO3
21  23.2       IV  CO(NH2)2
22  24.8       IV  Ca(NO3)2
23  26.7       IV     NaNO3
24  26.7       IV   Control

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p14 <- 
  ggplot(data = df14, mapping = aes(x = Trt, y = Yield)) + 
  geom_point() +
  geom_boxplot() +
  labs(x = "Treatment", y = "Yield") +
  theme_bw()
print(p14)

fm14 <- lm(formula = Yield ~ SoilType + Trt, data = df14)
summary(fm14)


Call:
lm(formula = Yield ~ SoilType + Trt, data = df14)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.0208 -2.4229  0.0792  2.1354  6.7958 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   35.354      2.826  12.511 2.44e-09 ***
SoilTypeII    -3.500      2.664  -1.314   0.2087    
SoilTypeIII   -4.233      2.664  -1.589   0.1329    
SoilTypeIV    -6.583      2.664  -2.471   0.0259 *  
TrtNH4NO3      1.050      3.263   0.322   0.7521    
TrtCO(NH2)2   -0.250      3.263  -0.077   0.9399    
TrtCa(NO3)2   -2.025      3.263  -0.621   0.5442    
TrtNaNO3      -2.600      3.263  -0.797   0.4380    
TrtControl    -1.700      3.263  -0.521   0.6100    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.615 on 15 degrees of freedom
Multiple R-squared:  0.3512,    Adjusted R-squared:  0.005215 
F-statistic: 1.015 on 8 and 15 DF,  p-value: 0.4653

anova(fm14)

Analysis of Variance Table

Response: Yield
          Df Sum Sq Mean Sq F value Pr(>F)
SoilType   3 133.62  44.539  2.0915 0.1443
Trt        5  39.31   7.862  0.3692 0.8618
Residuals 15 319.43  21.295

Latin Square Design

Used when experimental material is heterogenous in two perpendicular directions

Example

The following table shows the field layout and yield of a 5×5 Latin square experiment on the effect of spacing on yield of millet plants. Five levels of spacing were used. The data on yield (grams/plot) was recorded and is given below:

Yield <- c(
           257, 230, 279, 287, 202,
           245, 283, 245, 280, 260,
           182, 252, 280, 246, 250,
           203, 204, 227, 193, 259,
           231, 271, 266, 334, 338
           )
Row <- factor(x = rep(x = 1:5, each = 5))
Col <- factor(x = rep(x = 1:5, times = 5))
Trt <- c(
          "B", "E", "A", "C", "D"
        , "D", "A", "E", "B", "C"
        , "E", "B", "C", "D", "A"
        , "A", "C", "D", "E", "B"
        , "C", "D", "B", "A", "E"
         )

df15 <- data.frame(Yield, Row, Col, Trt)
df15

   Yield Row Col Trt
1    257   1   1   B
2    230   1   2   E
3    279   1   3   A
4    287   1   4   C
5    202   1   5   D
6    245   2   1   D
7    283   2   2   A
8    245   2   3   E
9    280   2   4   B
10   260   2   5   C
11   182   3   1   E
12   252   3   2   B
13   280   3   3   C
14   246   3   4   D
15   250   3   5   A
16   203   4   1   A
17   204   4   2   C
18   227   4   3   D
19   193   4   4   E
20   259   4   5   B
21   231   5   1   C
22   271   5   2   D
23   266   5   3   B
24   334   5   4   A
25   338   5   5   E

library(ggplot2)
# if (!require("ggplot2")) install.packages("ggplot2")
p15 <- 
  ggplot(data = df15, mapping = aes(x = Trt, y = Yield)) + 
  geom_point() +
  geom_boxplot() +
  labs(x = "Treatment", y = "Yield") +
  theme_bw()
print(p15)

fm15 <- lm(formula = Yield ~ Row + Col + Trt, data = df15)
summary(fm15)


Call:
lm(formula = Yield ~ Row + Col + Trt, data = df15)

Residuals:
   Min     1Q Median     3Q    Max 
-44.68 -12.48   1.12  16.52  54.92 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   240.08      23.43  10.247 2.75e-07 ***
Row2           11.60      20.55   0.565   0.5828    
Row3           -9.00      20.55  -0.438   0.6692    
Row4          -33.80      20.55  -1.645   0.1259    
Row5           37.00      20.55   1.801   0.0969 .  
Col2           24.40      20.55   1.187   0.2580    
Col3           35.80      20.55   1.742   0.1070    
Col4           44.40      20.55   2.161   0.0516 .  
Col5           38.20      20.55   1.859   0.0877 .  
TrtB           -7.00      20.55  -0.341   0.7393    
TrtC          -17.40      20.55  -0.847   0.4137    
TrtD          -31.60      20.55  -1.538   0.1500    
TrtE          -32.20      20.55  -1.567   0.1431    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 32.49 on 12 degrees of freedom
Multiple R-squared:  0.6536,    Adjusted R-squared:  0.3073 
F-statistic: 1.887 on 12 and 12 DF,  p-value: 0.1426

anova(fm15)

Analysis of Variance Table

Response: Yield
          Df  Sum Sq Mean Sq F value  Pr(>F)  
Row        4 13601.4  3400.3  3.2212 0.05164 .
Col        4  6146.2  1536.5  1.4556 0.27581  
Trt        4  4156.6  1039.1  0.9844 0.45229  
Residuals 12 12667.3  1055.6                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

All posts by date

Yield	Fert	Variety
51	80	V1
52	80	V1
53	90	V1
54	90	V1
56	100	V1
57	100	V1
55	80	V2
56	80	V2
58	90	V2
59	90	V2
62	100	V2
63	100	V2

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

Yield	Fert	Variety
51	80	V1
52	80	V1
53	90	V1
54	90	V1
56	100	V1
57	100	V1
55	80	V2
56	80	V2
58	90	V2
59	90	V2
62	100	V2
63	100	V2

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

Yield	Fert	Variety
51	80	V1
52	80	V1
53	90	V1
54	90	V1
56	100	V1
57	100	V1
55	80	V2
56	80	V2
58	90	V2
59	90	V2
62	100	V2
63	100	V2

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345

Leaf Area (cm^2)	Leaf Moisture (%)	Total Shoot Length (cm)
72	80	307
174	75	529
116	81	632
78	83	527
134	79	442
95	81	525
113	80	481
98	81	710
148	74	422
42	78	345