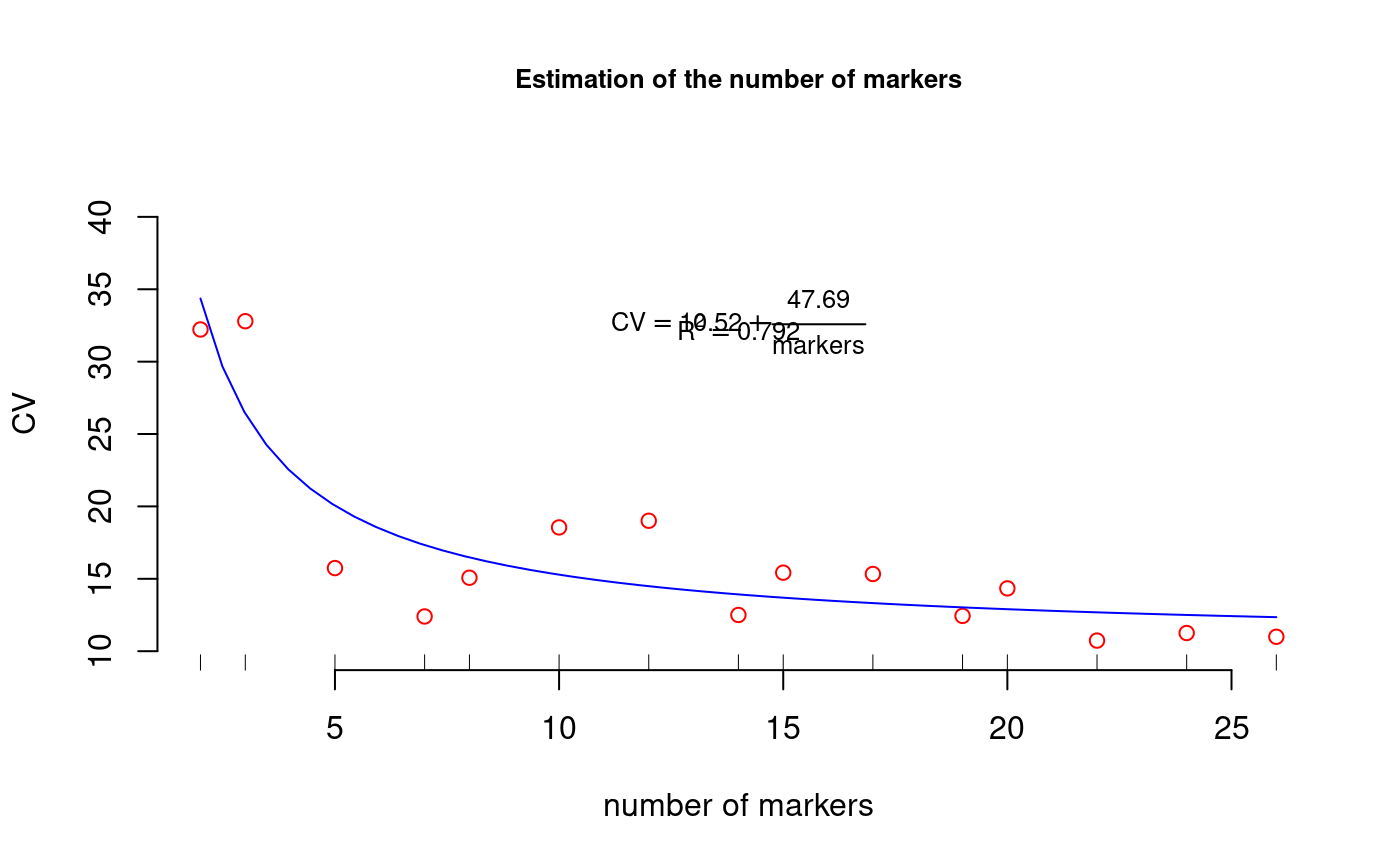
Resampling to find the optimal number of markers

Source: R/resampling.cv.R

This process finds the curve of CV for a different number of markers which allows us to determine the number of optimal markers for a given relative variability. A method of the curvature.

resampling.cv(A, size, npoints)

Arguments

A

data frame or matrix of binary data
size

number of re-samplings
npoints

Number of points to consider the model

Value

lm(formula = CV ~ I(1/marker))
Table with variation coefficient by number of markers

References

Efron, B., Tibshirani, R. (1993) An Introduction to the Boostrap. Chapman and Hall/CRC

See also

cv.similarity, similarity

Examples


library(agricolae)
#example table of molecular markers
data(markers)
study<-resampling.cv(markers,size=1,npoints=15)
#> 
#> Time of process ... 1.58146 
#
# Results of the model
summary(study$model)
#> 
#> Call:
#> lm(formula = CV ~ I(1/marker))
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#> -4.930 -1.686 -1.249  1.870  6.383 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   10.515      1.209   8.698 8.85e-07 ***
#> I(1/marker)   47.687      6.775   7.039 8.81e-06 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error: 3.281 on 13 degrees of freedom
#> Multiple R-squared:  0.7922,	Adjusted R-squared:  0.7762 
#> F-statistic: 49.55 on 1 and 13 DF,  p-value: 8.813e-06
#> 
coef<-coef(study$model)
py<-predict(study$model)
Rsq<-summary(study$model)$"r.squared"
table.cv <- data.frame(study$table.cv,estimate=py)
print(table.cv)
#>    marker       CV estimate
#> 1       2 32.22113 34.35873
#> 2       3 32.79360 26.41083
#> 3       5 15.73968 20.05251
#> 4       7 12.39719 17.32752
#> 5       8 15.07412 16.47596
#> 6      10 18.54876 15.28378
#> 7      12 19.00815 14.48899
#> 8      14 12.50055 13.92128
#> 9      15 15.42278 13.69420
#> 10     17 15.33190 13.32018
#> 11     19 12.43647 13.02490
#> 12     20 14.33746 12.89941
#> 13     22 10.73170 12.68264
#> 14     24 11.25340 12.50201
#> 15     26 10.99521 12.34917

# Plot CV
#startgraph
limy<-max(table.cv[,2])+10
plot(table.cv[,c(1,2)],col="red",frame=FALSE,xlab="number of markers",
ylim=c(10,limy), ylab="CV",cex.main=0.8,main="Estimation of the number of markers")
ty<-quantile(table.cv[,2],1)
tx<-median(table.cv[,1])
tz<-quantile(table.cv[,2],0.95)
text(tx,ty, cex=0.8,as.expression(substitute(CV == a + frac(b,markers),
list(a=round(coef[1],2),b=round(coef[2],2)))) )
text(tx,tz,cex=0.8,as.expression(substitute(R^2==r,list(r=round(Rsq,3)))))

# Plot CV = a + b/n.markers
fy<-function(x,a,b) a+b/x
x<-seq(2,max(table.cv[,1]),length=50)
y <- coef[1] + coef[2]/x
lines(x,y,col="blue")
#grid(col="brown")
rug(table.cv[,1])
#endgraph