Regression Analysis with Python
Introduction
- In God we trust, all others must bring data. (W. Edwards Deming)
- In Data we trust, all others must bring data.
Statistics
- Statistics is the science of uncertainty & variability
- Statistics turns data into information
- Data -> Information -> Knowledge -> Wisdom
- Data Driven Decisions (3Ds)
- Statistics is the interpretation of Science
- Statistics is the Art & Science of learning from data
Variable
- Characteristic that may vary from individual to individual
- Height, Weight, CGPA etc
Measurement
- Process of assigning numbers or labels to objects or states in accordance with logically accepted rules
Measurement Scales
- Nominal Scale: Obersvations may be classified into mutually exclusive & exhaustive classes or categories
- Ordinal Scale: Obersvations may be ranked
- Interval Scale: Difference between obersvations is meaningful
- Ratio Scale: Ratio between obersvations is meaningful & true zero point
Regression Analysis
- Quantifying dependency of a normal response on quantitative explanatory variable(s)
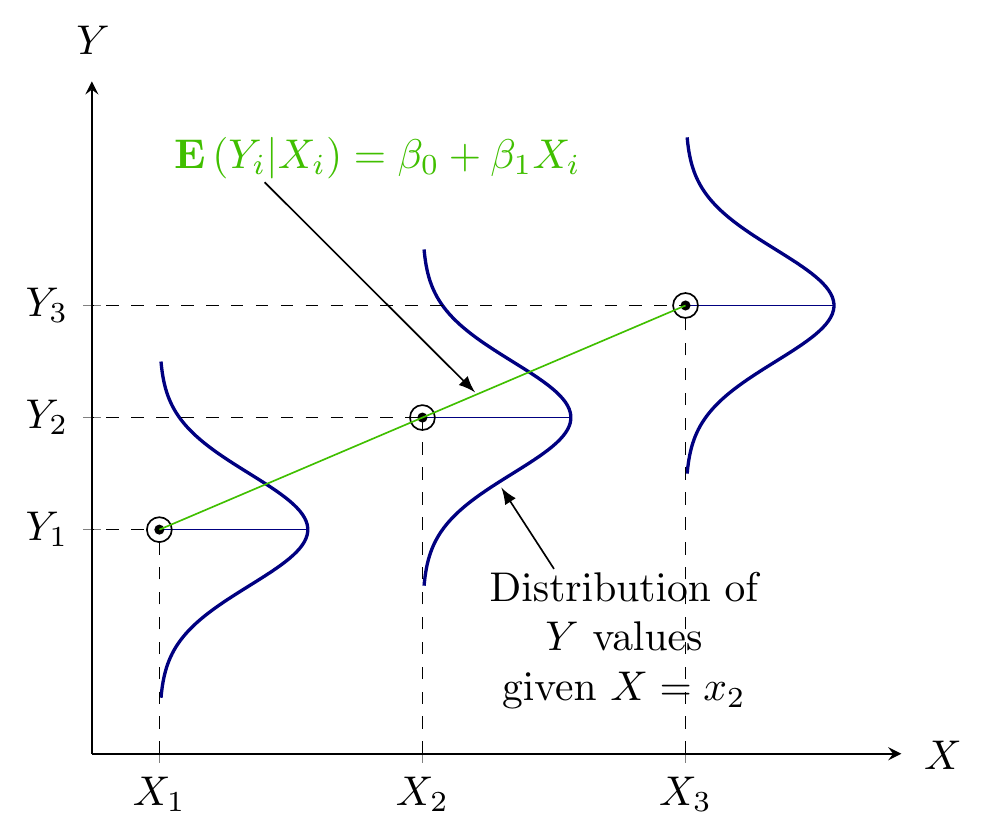
Figure 1: Population Regression Function
Simple Linear Regression
- Quantifying dependency of a normal response on a quantitative explanatory variable
Example
| Weekly Income ($) | Weekly Expenditures ($) |
|---|---|
| 80 | 70 |
| 100 | 65 |
| 120 | 90 |
| 140 | 95 |
| 160 | 110 |
| 180 | 115 |
| 200 | 120 |
| 220 | 140 |
| 240 | 155 |
| 260 | 150 |
Income = [80, 100, 120, 140, 160, 180, 200, 220, 240, 260]
Expend = [70, 65, 90, 95, 110, 115, 120, 140, 155, 150]import pandas as pd
df1 = pd.DataFrame(
{
"Income": Income
, "Expend": Expend
}
)
print(df1) Expend Income
0 70 80
1 65 100
2 90 120
3 95 140
4 110 160
5 115 180
6 120 200
7 140 220
8 155 240
9 150 260from matplotlib import pyplot as plt
fig = plt.figure()
plt.scatter(
df1["Income"]
, df1["Expend"]
, color = "green"
, marker = "o"
)
plt.title("Scatter plot of Weekly Income (\$) and Weekly Expenditures (\$)")
plt.xlabel("Weekly Income (\$)")
plt.ylabel("Weekly Expenditures (\$)")
plt.show()from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
Reg1 = ols(formula = "Expend ~ Income", data = df1)
Fit1 = Reg1.fit()
print(Fit1.summary()) OLS Regression Results
==============================================================================
Dep. Variable: Expend R-squared: 0.962
Model: OLS Adj. R-squared: 0.957
Method: Least Squares F-statistic: 202.9
Date: Tue, 02 Oct 2018 Prob (F-statistic): 5.75e-07
Time: 15:25:26 Log-Likelihood: -31.781
No. Observations: 10 AIC: 67.56
Df Residuals: 8 BIC: 68.17
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 24.4545 6.414 3.813 0.005 9.664 39.245
Income 0.5091 0.036 14.243 0.000 0.427 0.592
==============================================================================
Omnibus: 1.060 Durbin-Watson: 2.680
Prob(Omnibus): 0.589 Jarque-Bera (JB): 0.777
Skew: -0.398 Prob(JB): 0.678
Kurtosis: 1.891 Cond. No. 561.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.print(Fit1.params)Intercept 24.454545
Income 0.509091
dtype: float64print(Fit1.fittedvalues)0 65.181818
1 75.363636
2 85.545455
3 95.727273
4 105.909091
5 116.090909
6 126.272727
7 136.454545
8 146.636364
9 156.818182
dtype: float64print(Fit1.resid)0 4.818182
1 -10.363636
2 4.454545
3 -0.727273
4 4.090909
5 -1.090909
6 -6.272727
7 3.545455
8 8.363636
9 -6.818182
dtype: float64print(Fit1.bse)Intercept 6.413817
Income 0.035743
dtype: float64print(Fit1.centered_tss)8890.0print(anova_lm(Fit1)) df sum_sq mean_sq F PR(>F)
Income 1.0 8552.727273 8552.727273 202.867925 5.752746e-07
Residual 8.0 337.272727 42.159091 NaN NaNfig = plt.figure()
plt.scatter(
df1["Income"]
, df1["Expend"]
, color = "green"
, marker = "o"
)
plt.plot(df1["Income"], Fit1.fittedvalues)
plt.title("Regression plot of Weekly Income (\$) and Weekly Expenditures (\$)")
plt.xlabel("Weekly Income (\$)")
plt.ylabel("Weekly Expenditures (\$)")
plt.show()Multiple Linear Regression
- Quantifying dependency of a normal response on two or more quantitative explanatory variables
Example
| Fertilizer (Kg) | Rainfall (mm) | Yield (Kg) |
|---|---|---|
| 100 | 10 | 40 |
| 200 | 20 | 50 |
| 300 | 10 | 50 |
| 400 | 30 | 70 |
| 500 | 20 | 65 |
| 600 | 20 | 65 |
| 700 | 30 | 80 |
import numpy as np
Fertilizer = np.arange(100, 800, 100)
Rainfall = [10, 20, 10, 30, 20, 20, 30]
Yield = [40, 50, 50, 70, 65, 65, 80]import pandas as pd
df2 = pd.DataFrame(
{
"Fertilizer": Fertilizer
, "Rainfall": Rainfall
, "Yield": Yield
}
)
print(df2) Fertilizer Rainfall Yield
0 100 10 40
1 200 20 50
2 300 10 50
3 400 30 70
4 500 20 65
5 600 20 65
6 700 30 80from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection = "3d")
ax.scatter(
df2["Fertilizer"]
, df2["Rainfall"]
, df2["Yield"]
, color = "green"
, marker = "o"
, alpha = 1
)
ax.set_xlabel("Fertilizer")
ax.set_ylabel("Rainfall")
ax.set_zlabel("Yield")
plt.show()from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
Reg2 = ols(formula = "Yield ~ Fertilizer + Rainfall", data = df2)
Fit2 = Reg2.fit()
print(Fit2.summary()) OLS Regression Results
==============================================================================
Dep. Variable: Yield R-squared: 0.981
Model: OLS Adj. R-squared: 0.972
Method: Least Squares F-statistic: 105.3
Date: Tue, 02 Oct 2018 Prob (F-statistic): 0.000347
Time: 15:25:27 Log-Likelihood: -13.848
No. Observations: 7 AIC: 33.70
Df Residuals: 4 BIC: 33.53
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 28.0952 2.491 11.277 0.000 21.178 35.013
Fertilizer 0.0381 0.006 6.532 0.003 0.022 0.054
Rainfall 0.8333 0.154 5.401 0.006 0.405 1.262
==============================================================================
Omnibus: nan Durbin-Watson: 2.249
Prob(Omnibus): nan Jarque-Bera (JB): 0.705
Skew: -0.408 Prob(JB): 0.703
Kurtosis: 1.677 Cond. No. 1.28e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.28e+03. This might indicate that there are
strong multicollinearity or other numerical problems.print(Fit2.params)Intercept 28.095238
Fertilizer 0.038095
Rainfall 0.833333
dtype: float64print(Fit2.fittedvalues)0 40.238095
1 52.380952
2 47.857143
3 68.333333
4 63.809524
5 67.619048
6 79.761905
dtype: float64print(Fit2.resid)0 -0.238095
1 -2.380952
2 2.142857
3 1.666667
4 1.190476
5 -2.619048
6 0.238095
dtype: float64print(Fit2.bse)Intercept 2.491482
Fertilizer 0.005832
Rainfall 0.154303
dtype: float64print(Fit2.centered_tss)1150.0print(anova_lm(Fit2)) df sum_sq mean_sq F PR(>F)
Fertilizer 1.0 972.321429 972.321429 181.500000 0.000176
Rainfall 1.0 156.250000 156.250000 29.166667 0.005690
Residual 4.0 21.428571 5.357143 NaN NaNfrom mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from matplotlib import cm
fig = plt.figure()
ax = fig.add_subplot(111, projection = "3d")
ax.scatter(
df2["Fertilizer"]
, df2["Rainfall"]
, df2["Yield"]
, color = "green"
, marker = "o"
, alpha = 1
)
ax.set_xlabel("Fertilizer")
ax.set_ylabel("Rainfall")
ax.set_zlabel("Yield")
x_surf = np.arange(100, 720, 20)
y_surf = np.arange(10, 32, 2)
x_surf, y_surf = np.meshgrid(x_surf, y_surf)
exog = pd.core.frame.DataFrame({
"Fertilizer": x_surf.ravel()
, "Rainfall": y_surf.ravel()
})
out = Fit2.predict(exog = exog)
ax.plot_surface(
x_surf
, y_surf
, out.reshape(x_surf.shape)
, rstride=1
, cstride=1
, color="None"
, alpha = 0.4
)
plt.show()Polynomial Regression Analysis
- Quantifying non-linear dependency of a normal response on quantitative explanatory variable(s)
Example
An experiment was conducted to evaluate the effects of different levels of nitrogen. Three levels of nitrogen: 0, 10 and 20 grams per plot were used in the experiment. Each treatment was replicated twice and data is given below:
| Nitrogen | Yield |
|---|---|
| 0 | 5 |
| 0 | 7 |
| 10 | 15 |
| 10 | 17 |
| 20 | 9 |
| 20 | 11 |
Nitrogen = [0, 0, 10, 10, 20, 20]
Yield = [5, 7, 15, 17, 9, 11]import pandas as pd
df3 = pd.DataFrame(
{
"Nitrogen": Nitrogen
, "Yield": Yield
}
)
print(df3) Nitrogen Yield
0 0 5
1 0 7
2 10 15
3 10 17
4 20 9
5 20 11from matplotlib import pyplot as plt
fig = plt.figure()
plt.scatter(
df3["Nitrogen"]
, df3["Yield"]
, color = "green"
, marker = "o"
)
plt.title("Scatter plot of Nitrogen and Yield")
plt.xlabel("Nitrogen")
plt.ylabel("Yield")
plt.show()from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
Reg3 = ols(formula = "Yield ~ Nitrogen + I(Nitrogen**2)", data = df3)
Fit3 = Reg3.fit()
print(Fit3.summary()) OLS Regression Results
==============================================================================
Dep. Variable: Yield R-squared: 0.944
Model: OLS Adj. R-squared: 0.907
Method: Least Squares F-statistic: 25.33
Date: Tue, 02 Oct 2018 Prob (F-statistic): 0.0132
Time: 15:25:27 Log-Likelihood: -8.5136
No. Observations: 6 AIC: 23.03
Df Residuals: 3 BIC: 22.40
Df Model: 2
Covariance Type: nonrobust
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
Intercept 6.0000 1.000 6.000 0.009 2.818 9.182
Nitrogen 1.8000 0.255 7.060 0.006 0.989 2.611
I(Nitrogen ** 2) -0.0800 0.012 -6.532 0.007 -0.119 -0.041
==============================================================================
Omnibus: nan Durbin-Watson: 3.333
Prob(Omnibus): nan Jarque-Bera (JB): 1.000
Skew: 0.000 Prob(JB): 0.607
Kurtosis: 1.000 Cond. No. 418.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.print(Fit3.params)Intercept 6.00
Nitrogen 1.80
I(Nitrogen ** 2) -0.08
dtype: float64print(Fit3.fittedvalues)0 6.0
1 6.0
2 16.0
3 16.0
4 10.0
5 10.0
dtype: float64print(Fit3.resid)0 -1.0
1 1.0
2 -1.0
3 1.0
4 -1.0
5 1.0
dtype: float64print(Fit3.bse)Intercept 1.000000
Nitrogen 0.254951
I(Nitrogen ** 2) 0.012247
dtype: float64print(Fit3.centered_tss)107.333333333print(anova_lm(Fit3)) df sum_sq mean_sq F PR(>F)
Nitrogen 1.0 16.000000 16.000000 8.000000 0.066276
I(Nitrogen ** 2) 1.0 85.333333 85.333333 42.666667 0.007292
Residual 3.0 6.000000 2.000000 NaN NaNfig = plt.figure()
plt.scatter(
df3["Nitrogen"]
, df3["Yield"]
, color = "green"
, marker = "o"
)
plt.plot(df3["Nitrogen"], Fit3.fittedvalues)
plt.title("Regression plot of Nitrogen and Yield")
plt.xlabel("Nitrogen")
plt.ylabel("Yield")
plt.show()