An Introduction to Statistics using SPSS

Blogs

Data Science, Statistics, Research, SPSS

Introduction

alt text

 

Statistics

  • Statistics is the science of uncertainty & variability
  • Statistics turns data into information
  • Data -> Information -> Knowledge -> Wisdom
  • Statistics is the interpretation of Science
  • Statistics is the Art & Science of learning from data

 

Variable

  • Characteristic that may vary from individual to individual

 

Measurement

  • Process of assigning numbers or labels to objects or states in accordance with logically accepted rules

 

Measurement Scales

  • Nominal Scale: Obersvations may be classified into mutually exclusive & exhaustive categories
  • Ordinal Scale: Obersvations may be ranked
  • Interval Scale: Difference between obersvations is meaningful
  • Ratio Scale: Ratio between obersvations is meaningful & true zero point

 

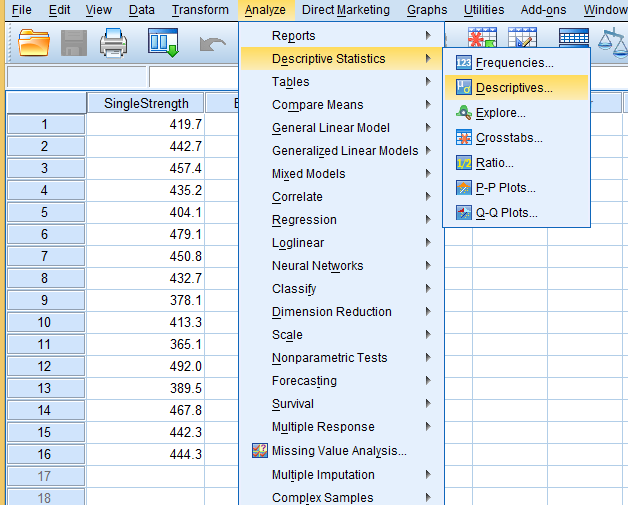
Descriptive Statistics

  • No of observations
  • Measures of Central Tendency
  • Measures of Dispersion
  • Measures of Skewness
  • Measures of Kurtosis

 

Example

Following data presents a subset of Yarn strength and Elongation percentage from an experiment to test yarn strength and extension of blue jeans designed under Conducted in Sudan Textile Factory Method.

 

Single Strength Elongation
419.7 3.22
442.7 2.78
457.4 1.60
435.2 1.88
404.1 1.88
479.1 2.34
450.8 2.44
432.7 2.12
378.1 2.88
413.3 2.37
365.1 1.40
492.0 2.02
389.5 2.02
467.8 1.92
442.3 2.44
444.3 1.74

Reference

Mousa, A.H.N. (1978). Analysis of the Effect of Size Formulation Variations on Yarn Tenacity and Elongation. Textile Research Journal, 48, 713-717.

 

alt text

 

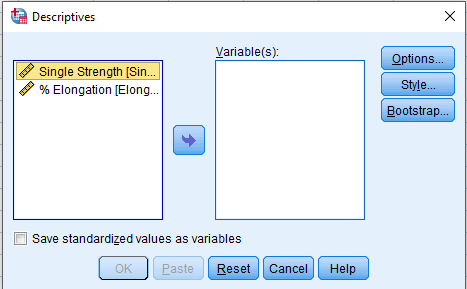
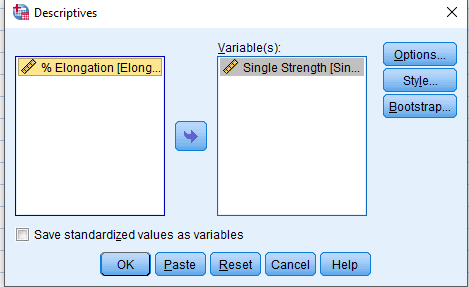
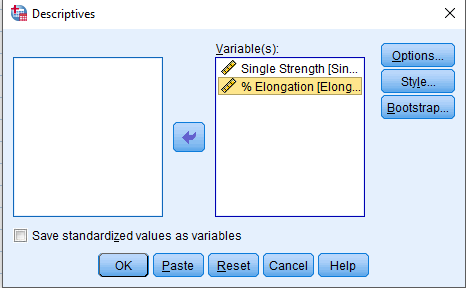
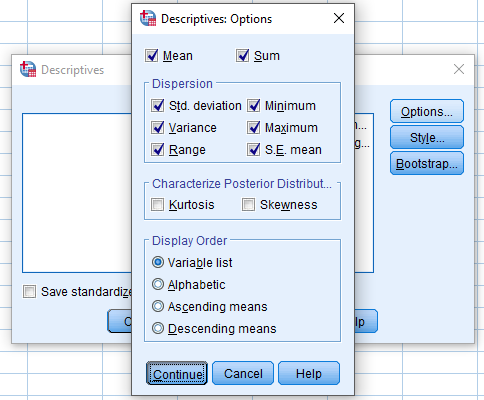
Analyze > Descriptive Statistics > Descriptives …

 

alt text
alt text
alt text
alt text
alt text
alt text

 

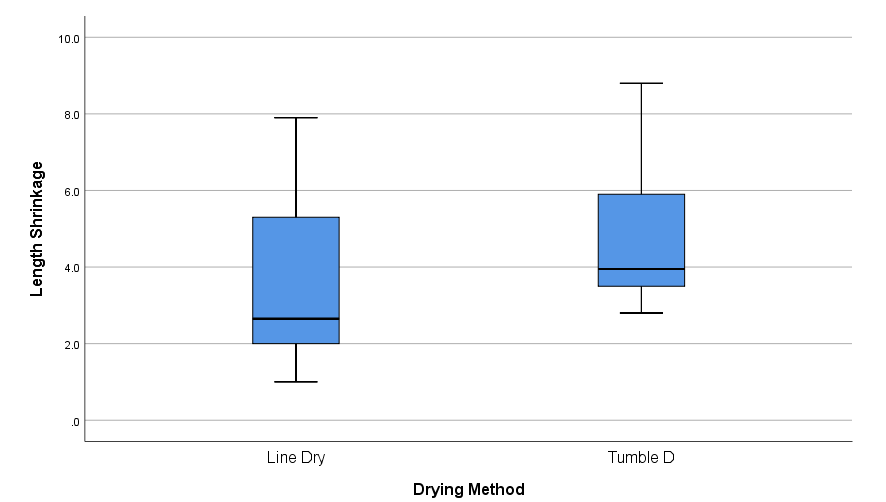
Boxwhisker Diagram

  • Pictorial display of five number summary (Minimum, Q1, Q2, Q3 and Maximum)

 

Example

Effact of Two drying methods (Line Dry and Tumble Dry) are to be compared for some kind of shrinkage of some particular brand of fabric. Following data was observed from an experiment:

Drying Method Length Shrinkage Drying Method Length Shrinkage
Line Dry 1.0 Tumble Dry 2.8
Line Dry 1.5 Tumble Dry 3.0
Line Dry 2.1 Tumble Dry 3.0
Line Dry 2.1 Tumble Dry 2.9
Line Dry 5.4 Tumble Dry 6.8
Line Dry 5.4 Tumble Dry 6.5
Line Dry 2.8 Tumble Dry 2.9
Line Dry 3.0 Tumble Dry 3.6
Line Dry 1.4 Tumble Dry 3.5
Line Dry 1.8 Tumble Dry 3.7
Line Dry 2.3 Tumble Dry 3.5
Line Dry 2.2 Tumble Dry 3.5
Line Dry 7.0 Tumble Dry 7.9
Line Dry 7.2 Tumble Dry 8.0
Line Dry 4.2 Tumble Dry 4.0
Line Dry 4.5 Tumble Dry 4.8
Line Dry 1.8 Tumble Dry 4.0
Line Dry 1.9 Tumble Dry 4.2
Line Dry 2.5 Tumble Dry 3.9
Line Dry 2.2 Tumble Dry 3.7
Line Dry 7.5 Tumble Dry 8.6
Line Dry 7.9 Tumble Dry 8.8
Line Dry 4.8 Tumble Dry 4.7
Line Dry 5.2 Tumble Dry 5.3

 

Reference

Higgins, L., Anand, S.C., Holmes, D.A., Hall, M.E., and Underly, K. (2003). Effects of Various Home Laundering on the Dimensional Stability, Wrinkling, and Other Properties of Plain Woven Cotton Fabrics: Part II: Effect of Rinse Cycle Softener and Drying Method and of Tumble Sheet Softener and Tumble Drying Time. Textile Research Journal, 73, 407-420.

 

alt text

 

Graphs > Legacy Dialogs > Boxplot …

 

alt text
alt text
alt text
alt text

 

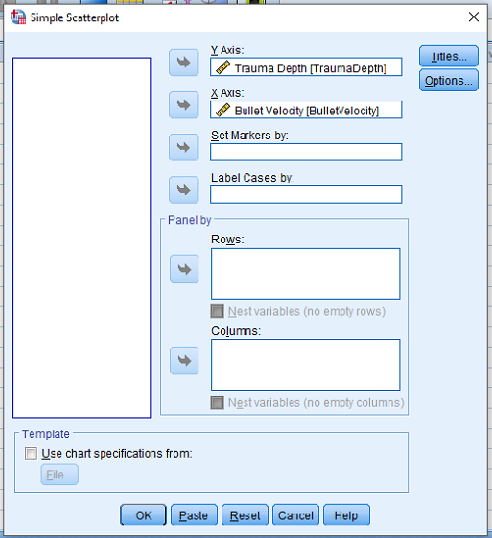
Scatter Plot

  • Two dimensional graph to show the relationship among two variables

 

Example

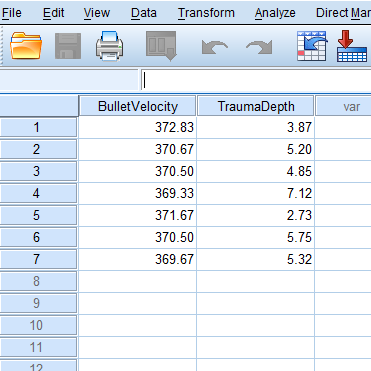
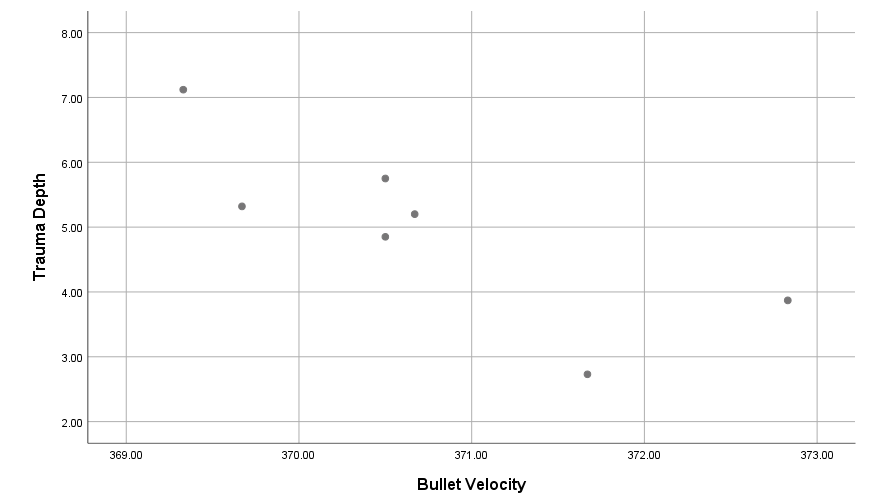
An Experiment was conducted to test ballistic tests for some fabric. To test the effect, bullet volicity and depth of trauma was observed. Some obser vations as example are given in the following table. Each measurement is based on 6 replicates.

Bullet Velocity Trauma Depth
372.83 3.87
370.67 5.20
370.50 4.85
369.33 7.12
371.67 2.73
370.50 5.75
369.67 5.32

 

Reference

Karahan, M. (2008). Comparison of Ballistic Performance and Energy Absorption Capabilities of Woven and Unidirectional Aramid Fabrics. Textile Research Journal, 78, 718-730.

 

alt text

 

Graphs > Legacy Dialogs > Scatter/Dot …

 

alt text
alt text
alt text
alt text

 

Regression Analysis

  • Quantifying dependency of a normal response on quantitative explanatory variable(s)

 

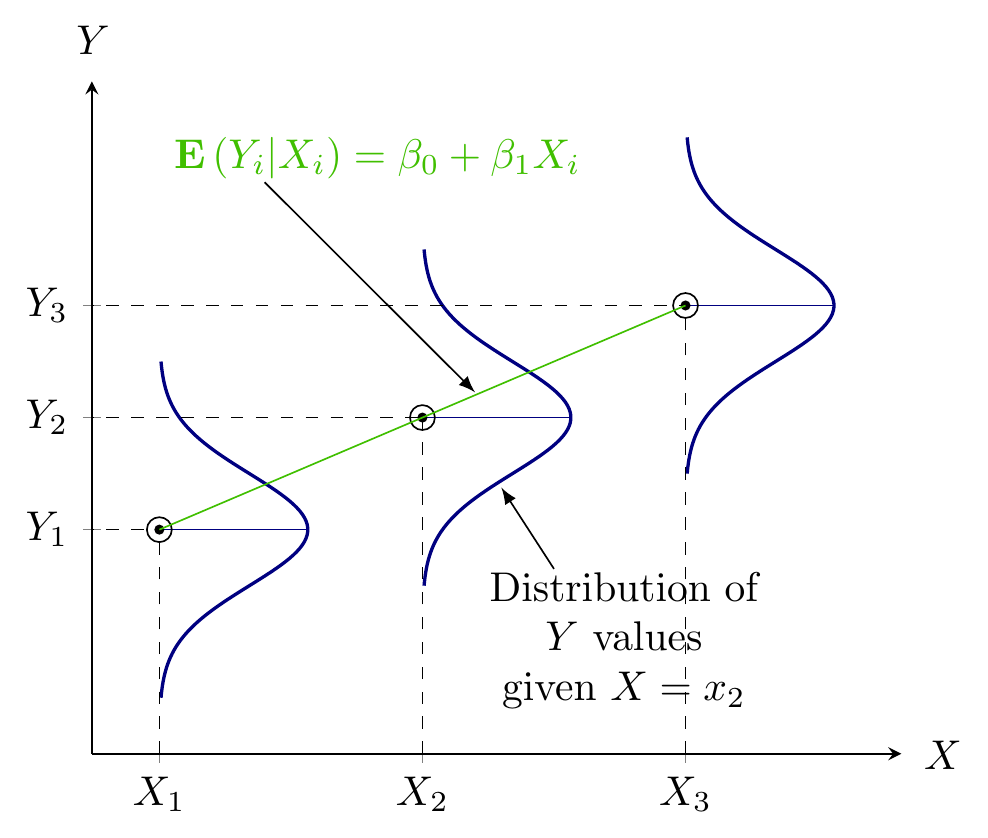
alt text

 

Simple Linear Regression

  • Quantifying dependency of a normal response on a quantitative explanatory variable

 

Example

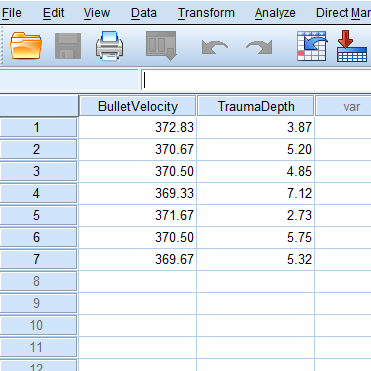
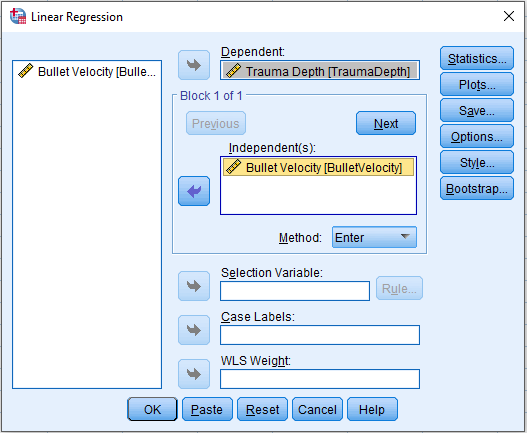
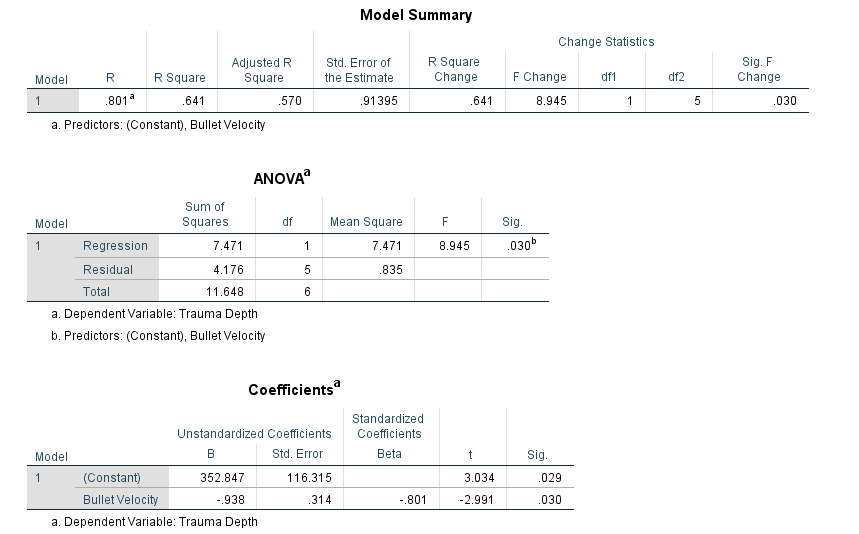
An Experiment was conducted to test ballistic tests for some fabric. To test the effect, bullet volicity and depth of trauma was observed. Some obser vations as example are given in the following table. Each measurement is based on 6 replicates.

Bullet Velocity Trauma Depth
372.83 3.87
370.67 5.20
370.50 4.85
369.33 7.12
371.67 2.73
370.50 5.75
369.67 5.32

 

Reference

Karahan, M. (2008). Comparison of Ballistic Performance and Energy Absorption Capabilities of Woven and Unidirectional Aramid Fabrics. Textile Research Journal, 78, 718-730.

 

alt text

 

Analyze > Regression > Linear …

 

alt text
alt text
alt text
alt text

 

Multiple Linear Regression

  • Quantifying dependency of a normal response on two or more quantitative explanatory variables

 

Example

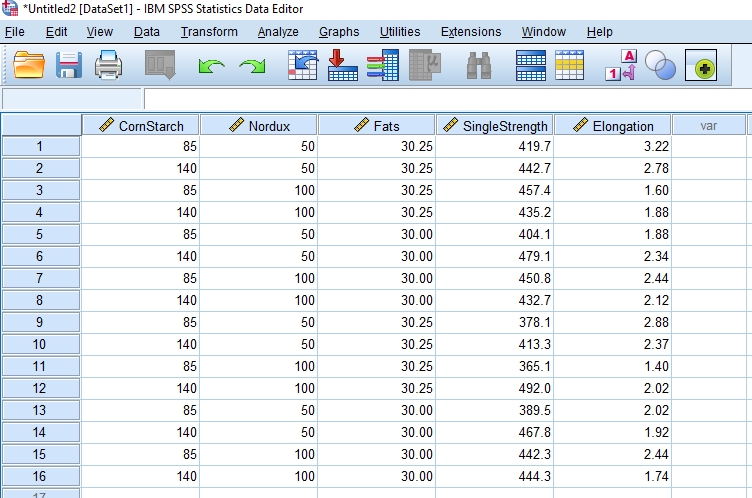
Following data presents a Factorial experiment relating yarn strength and elongation to 3 factors: Corn Starch, Nordux, and Fats. Conducted in Sudan Textile Factory Method.

Corn Starch Nordux Fats Single Strength Enolgation
85 50 30.25 419.7 3.22
140 50 30.25 442.7 2.78
85 100 30.25 457.4 1.60
140 100 30.25 435.2 1.88
85 50 30.00 404.1 1.88
140 50 30.00 479.1 2.34
85 100 30.00 450.8 2.44
140 100 30.00 432.7 2.12
85 50 30.25 378.1 2.88
140 50 30.25 413.3 2.37
85 100 30.25 365.1 1.40
140 100 30.25 492.0 2.02
85 50 30.00 389.5 2.02
140 50 30.00 467.8 1.92
85 100 30.00 442.3 2.44
140 100 30.00 444.3 1.74

Reference

Mousa, A.H.N. (1978). Analysis of the Effect of Size Formulation Variations on Yarn Tenacity and Elongation. Textile Research Journal, 48, 713-717.

 

alt text

 

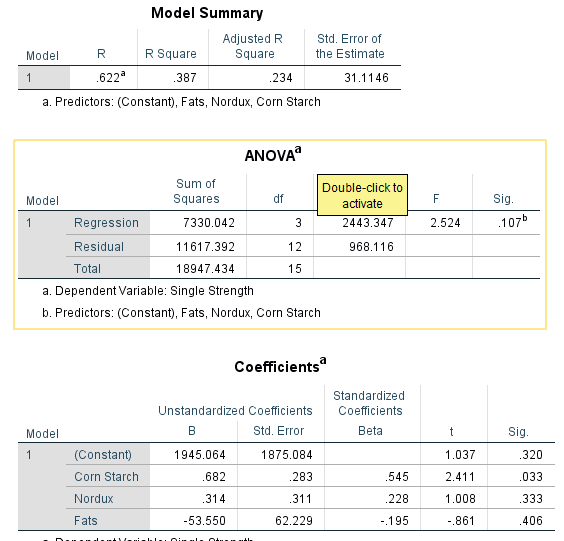
Analyze > Regression > Linear …

 

alt text
alt text
alt text

 

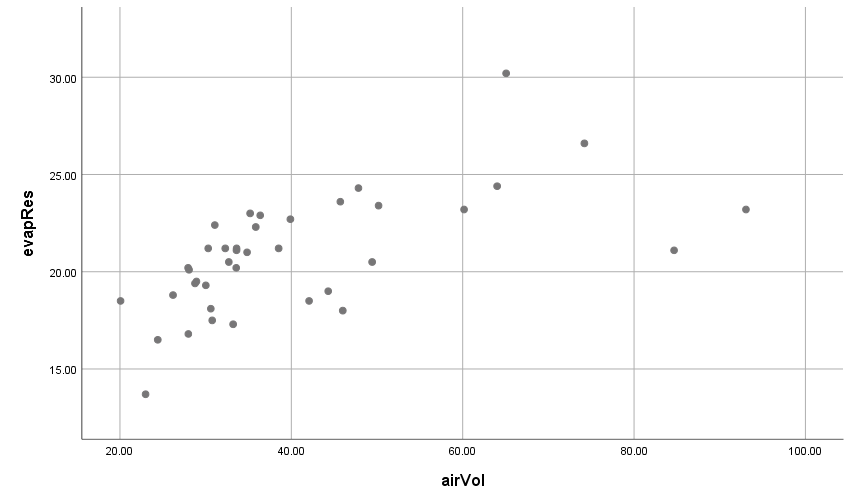
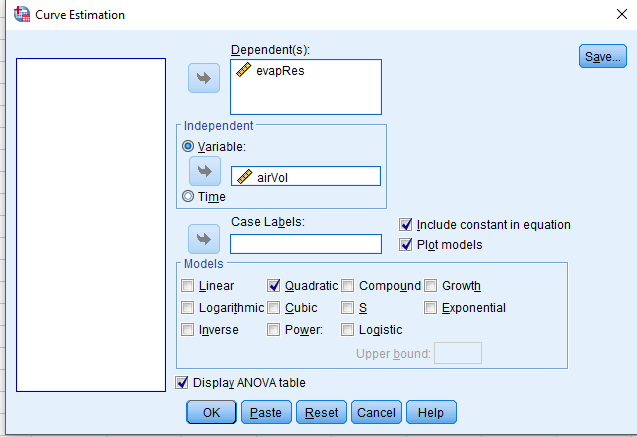
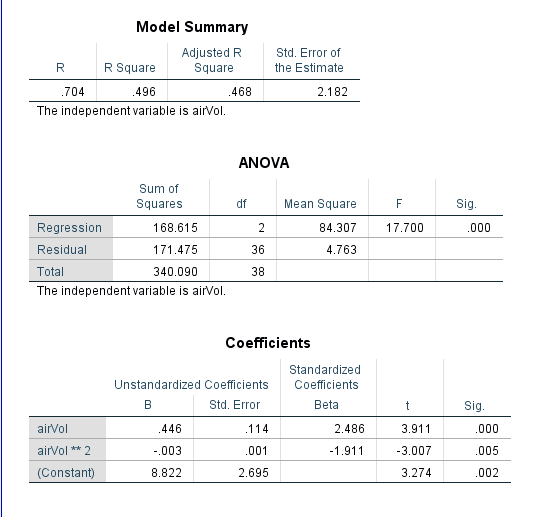
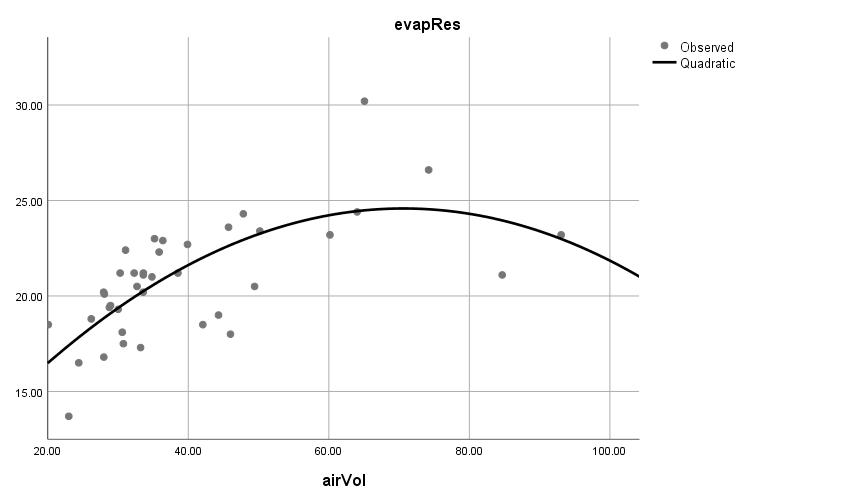
Polynomial Regression Analysis

  • Quantifying non-linear dependency of a normal response on quantitative explanatory variable(s)

Example

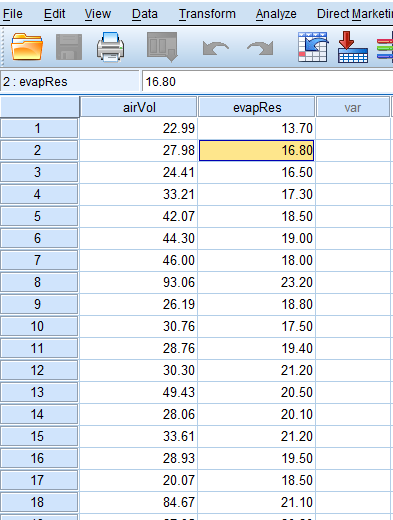
The Relationship Between Air Layers and Evaporative Resistance of Male Chinese Clothing is to be observed from Measurements of total air volume and total evaporative resistance of 39 Chinese clothing ensembles the following data.

Air Volume Evaporative Resistance Air Volume Evaporative Resistance
22.99 13.7 32.29 21.2
27.98 16.8 33.60 21.1
24.41 16.5 34.83 21.0
33.21 17.3 36.37 22.9
42.07 18.5 38.52 21.2
44.30 19.0 30.02 19.3
46.00 18.0 50.18 23.4
93.06 23.2 32.70 20.5
26.19 18.8 33.57 20.2
30.76 17.5 64.02 24.4
28.76 19.4 60.16 23.2
30.30 21.2 35.85 22.3
49.43 20.5 39.89 22.7
28.06 20.1 47.83 24.3
33.61 21.2 30.60 18.1
28.93 19.5 35.19 23.0
20.07 18.5 45.72 23.6
84.67 21.1 74.20 26.6
27.95 20.2 65.07 30.2
31.07 22.4

 

Reference

Wang, F., Peng, H., and Shi, W. (2016). The Relationship Between Air Layers and Evaporative Resistance of Male Chinese Clothing. Applied Ergonomics, 56, 194-202.

 

alt text
alt text

 

Analyze > Regression > Curve Estimation …

 

alt text
alt text
alt text
alt text

 

Analysis of Variance (ANOVA)

  • Comparing means of Normal dependent variable for levels of different factor(s)

 

alt text

 

Example

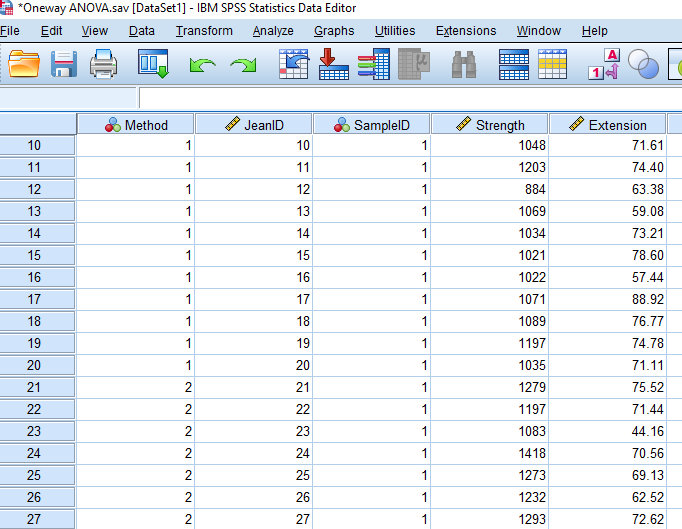
Experiment comparing tensile strength and extension of blue jeans that were designed manually and with laser beams. Data from 20 pairs of jeans per design method is presented in the table.

Method Jean ID Sample ID Strength Extension
1 1 1 1266 68.06
1 2 1 1099 61.54
1 3 1 1068 40.48
1 4 1 1266 59.83
1 5 1 968 55.89
1 6 1 1039 54.12
1 7 1 1194 77.09
1 8 1 926 61.80
1 9 1 1009 58.31
1 10 1 1048 71.61
1 11 1 1203 74.40
1 12 1 884 63.38
1 13 1 1069 59.08
1 14 1 1034 73.21
1 15 1 1021 78.60
1 16 1 1022 57.44
1 17 1 1071 88.92
1 18 1 1089 76.77
1 19 1 1197 74.78
1 20 1 1035 71.11
2 21 1 1279 75.52
2 22 1 1197 71.44
2 23 1 1083 44.16
2 24 1 1418 70.56
2 25 1 1273 69.13
2 26 1 1232 62.52
2 27 1 1293 72.62
2 28 1 1121 68.96
2 29 1 1286 71.03
2 30 1 1416 69.34
2 31 1 1285 81.79
2 32 1 1268 69.29
2 33 1 1365 73.73
2 34 1 1309 75.01
2 35 1 1343 75.95
2 36 1 1292 72.64
2 37 1 1234 73.73
2 38 1 1226 75.97
2 39 1 1229 71.60
2 40 1 1254 70.48
1 1 2 1140 63.04
1 2 2 1104 65.20
1 3 2 1051 50.62
1 4 2 1128 56.21
1 5 2 1044 53.51
1 6 2 1303 59.53
1 7 2 1081 60.75
1 8 2 958 60.60
1 9 2 1058 69.80
1 10 2 1077 62.05
1 11 2 956 72.87
1 12 2 1010 59.41
1 13 2 1062 61.71
1 14 2 1073 71.51
1 15 2 1027 68.16
1 16 2 1048 60.76
1 17 2 1101 63.70
1 18 2 1076 80.69
1 19 2 1081 69.65
1 20 2 1084 68.45
2 21 2 1205 71.44
2 22 2 1214 69.00
2 23 2 1055 47.05
2 24 2 1402 74.50
2 25 2 1310 72.76
2 26 2 1324 73.01
2 27 2 1303 79.82
2 28 2 1083 65.43
2 29 2 1391 69.84
2 30 2 1225 74.16
2 31 2 1396 79.49
2 32 2 1273 75.30
2 33 2 1326 66.65
2 34 2 1393 79.21
2 35 2 1172 73.57
2 36 2 1241 71.80
2 37 2 1292 77.70
2 38 2 1354 73.83
2 39 2 1299 73.59
2 40 2 1202 68.45
1 1 3 1104 61.40
1 2 3 1113 63.44
1 3 3 1063 50.48
1 4 3 1200 63.08
1 5 3 1006 66.70
1 6 3 860 46.39
1 7 3 936 62.76
1 8 3 967 64.72
1 9 3 1018 61.55
1 10 3 1191 69.50
1 11 3 987 73.45
1 12 3 1155 79.59
1 13 3 982 57.91
1 14 3 1064 70.86
1 15 3 1112 68.17
1 16 3 1040 63.46
1 17 3 1075 61.44
1 18 3 1081 73.51
1 19 3 1045 71.19
1 20 3 1077 69.33
2 21 3 1283 78.62
2 22 3 1154 63.06
2 23 3 1117 42.43
2 24 3 1335 71.45
2 25 3 1277 73.41
2 26 3 1313 71.44
2 27 3 1361 74.27
2 28 3 1104 70.42
2 29 3 1450 72.40
2 30 3 1323 75.00
2 31 3 1315 74.82
2 32 3 1321 77.76
2 33 3 1315 66.90
2 34 3 1386 77.64
2 35 3 1165 75.60
2 36 3 1198 69.73
2 37 3 1223 69.42
2 38 3 1289 80.39
2 39 3 1339 71.40
2 40 3 1266 72.36

 

Reference

Ondogan, Z., Pamuk, O., Ondogan, E.N., and Ozguney, A. (2005). Improving the Appearance of All Textile Products from Clothing to Home Textile Using Laser Technology. Optics and Laser Technology, 37, 631-637.

 

alt text

 

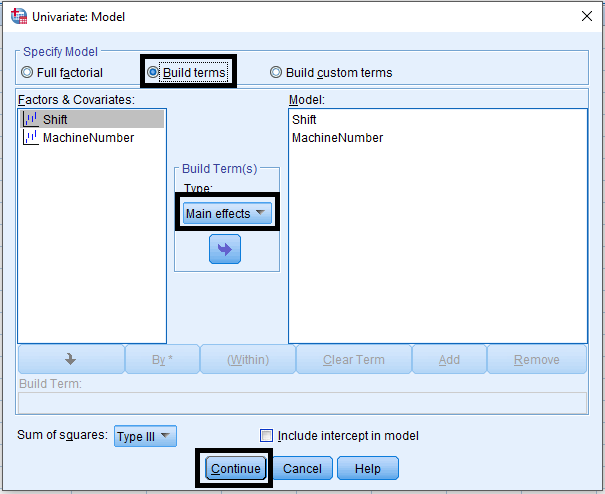
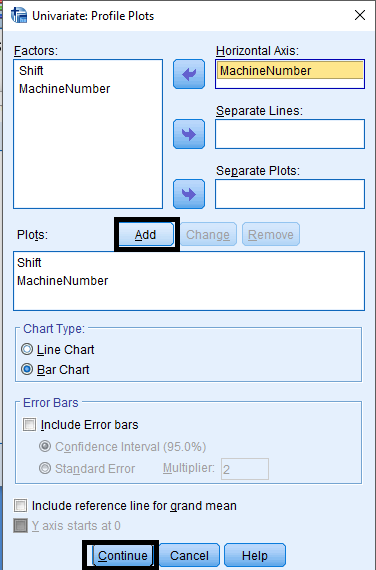
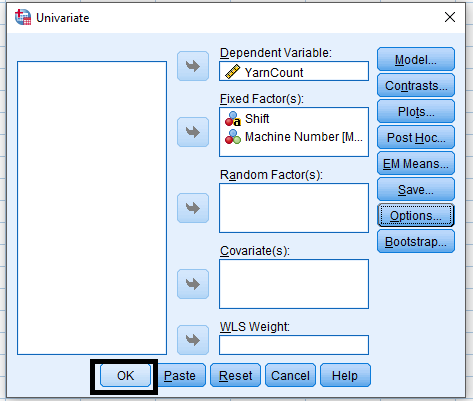
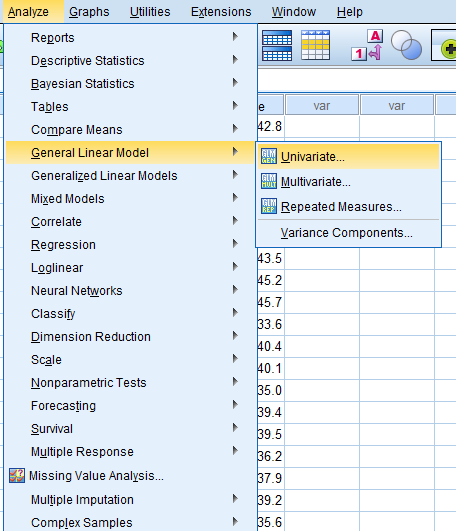
Analyze > General Linear Model > Univariate …

 

alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text

 

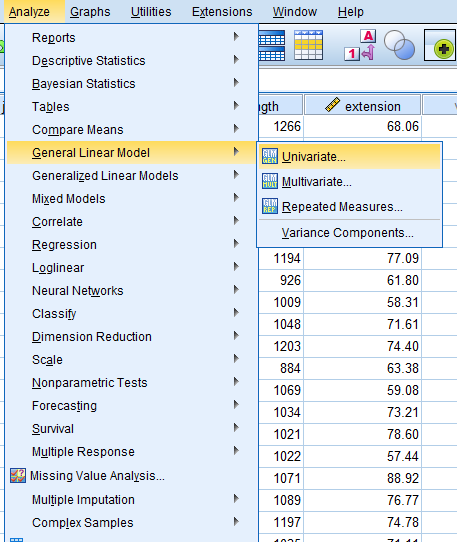
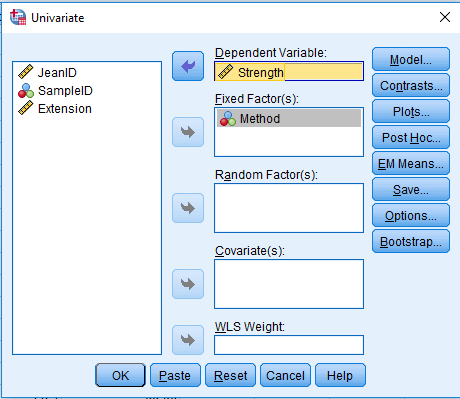
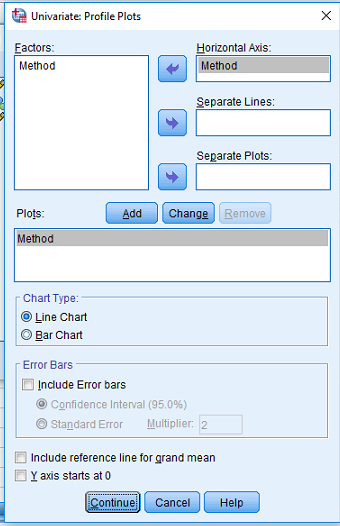
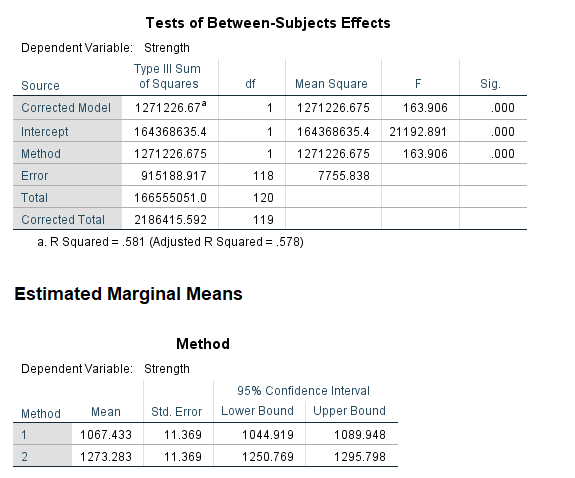
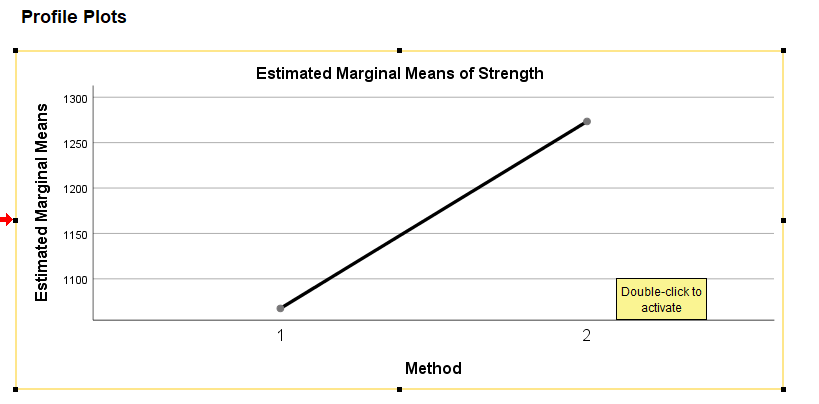
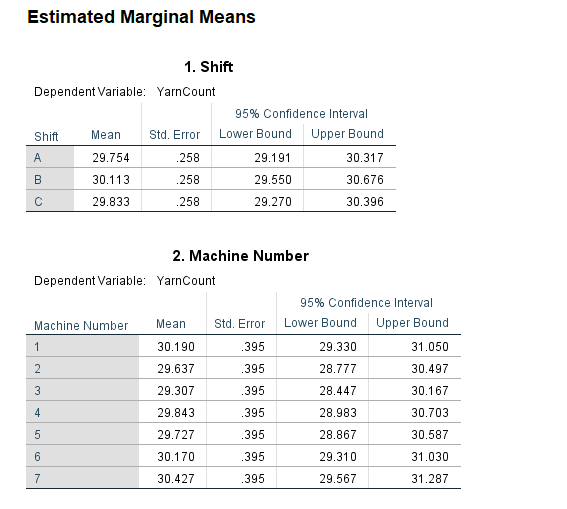
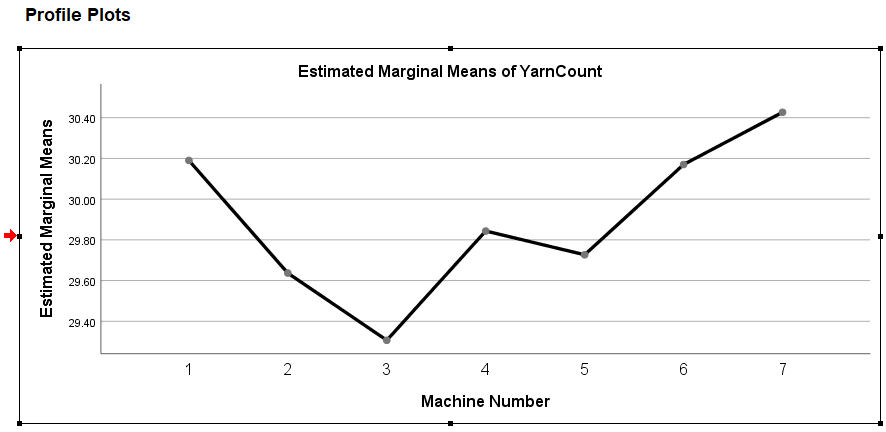
Example

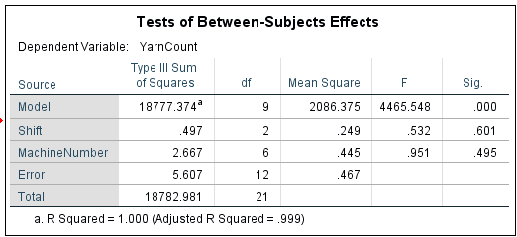
The analysis of variance of cotton yarn fineness is customer satisfaction with quality textile product. The purpose of this study is to minimize the faults of finished cotton fabric by maintaining actual yarn count during producing in ring frame. If the analysis shows the mean count difference due to shift and machine number then action should be taken to maintain required count of yarn. This action may be taken by setting of actual draft, uniform linear density of finisher draw frame sliver and maintaining proper atmospheric condition in ring and back section. The 210 data for yarn count of 30 KH (30 carded Hosiery) was summarized as follows:

Machine Number Shift YarnCount
1 A 29.52
2 A 29.58
3 A 28.62
4 A 30.50
5 A 29.03
6 A 29.75
7 A 31.28
1 B 30.91
2 B 29.33
3 B 29.32
4 B 30.04
5 B 30.33
6 B 30.91
7 B 29.95
1 C 30.14
2 C 30.00
3 C 29.98
4 C 28.99
5 C 29.82
6 C 29.85
7 C 30.05

 

Reference

Hossen, J., Haque, E., Khan, S.K., and Saha, S. (2012). Analysis of cotton yarn count variation by two way ANOVA. Conference: Annals of the University of Oradea, Fascicle of Textiles, Leatherwork. At Annals of the University of Oradea, XIII-02.

 

alt text

 

Analyze > General Linear Model > Univariate …

 

alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text

 

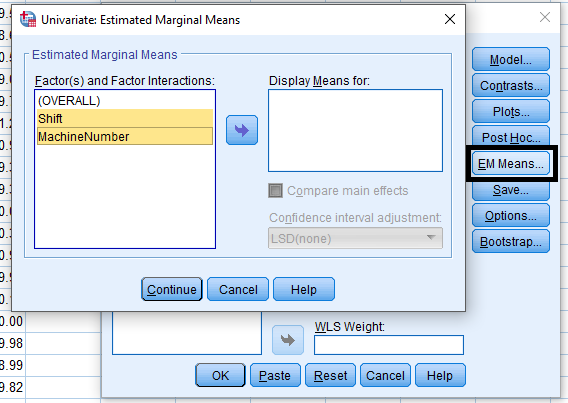
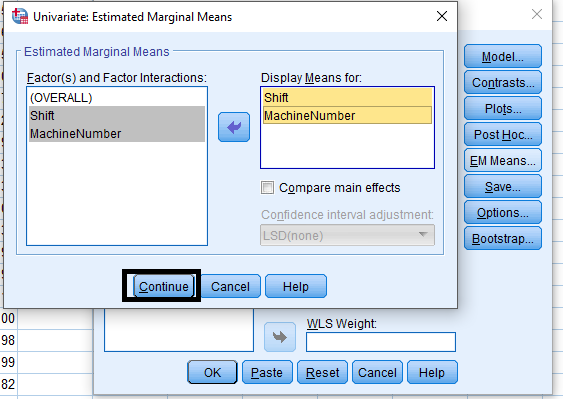
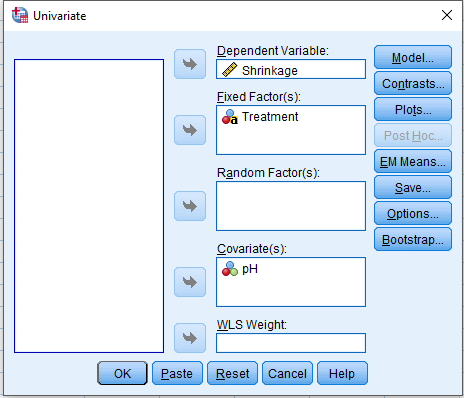
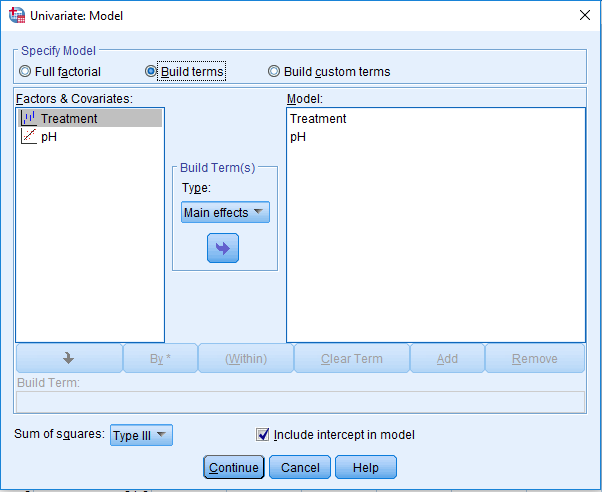
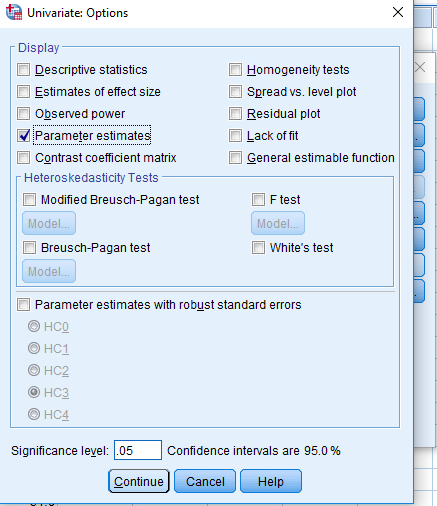
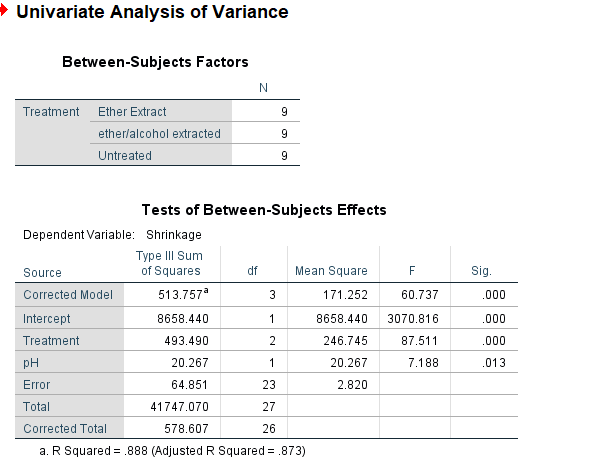
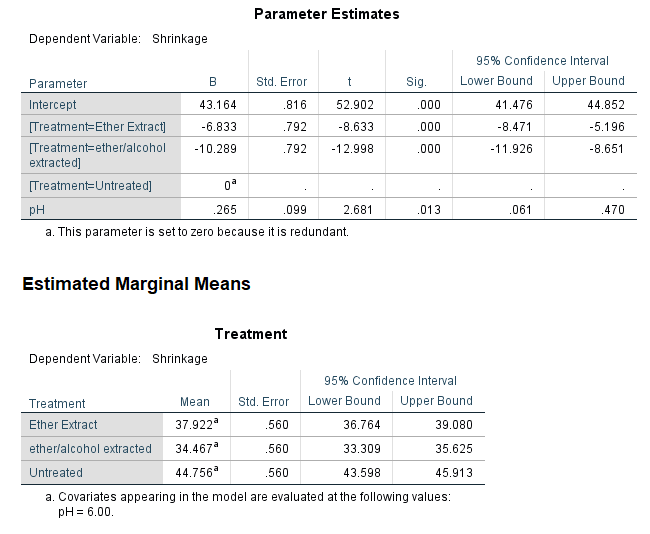
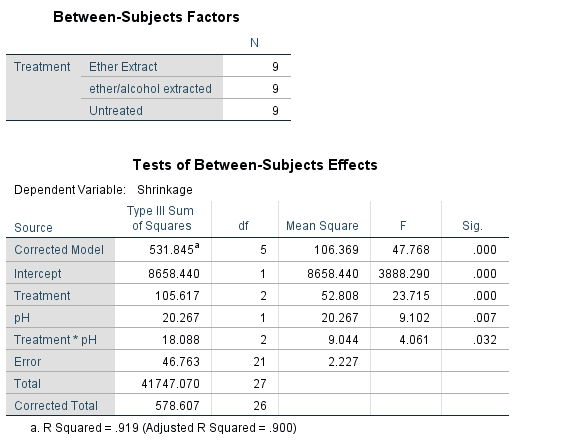
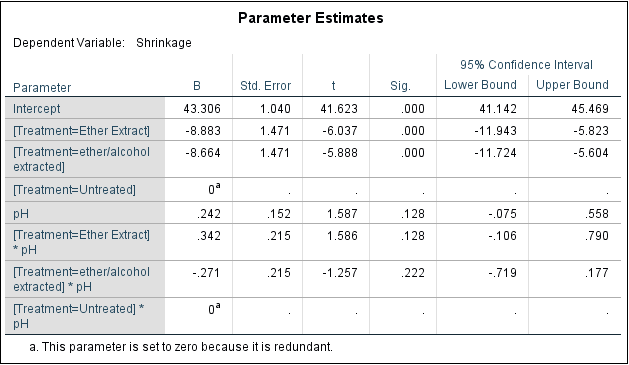
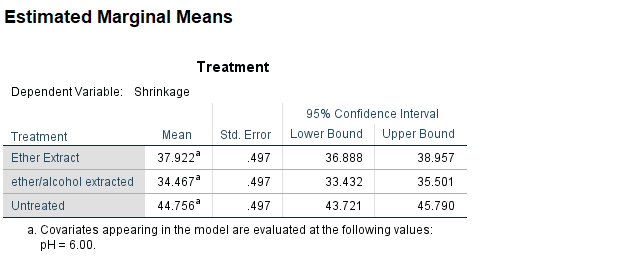
Analysis of Covariance (ANCOVA)

  • Quantifying dependency of a normal response on quantitative explanatory variable(s)
  • Comparing means of Normal dependent variable for levels of different factor(s)

 

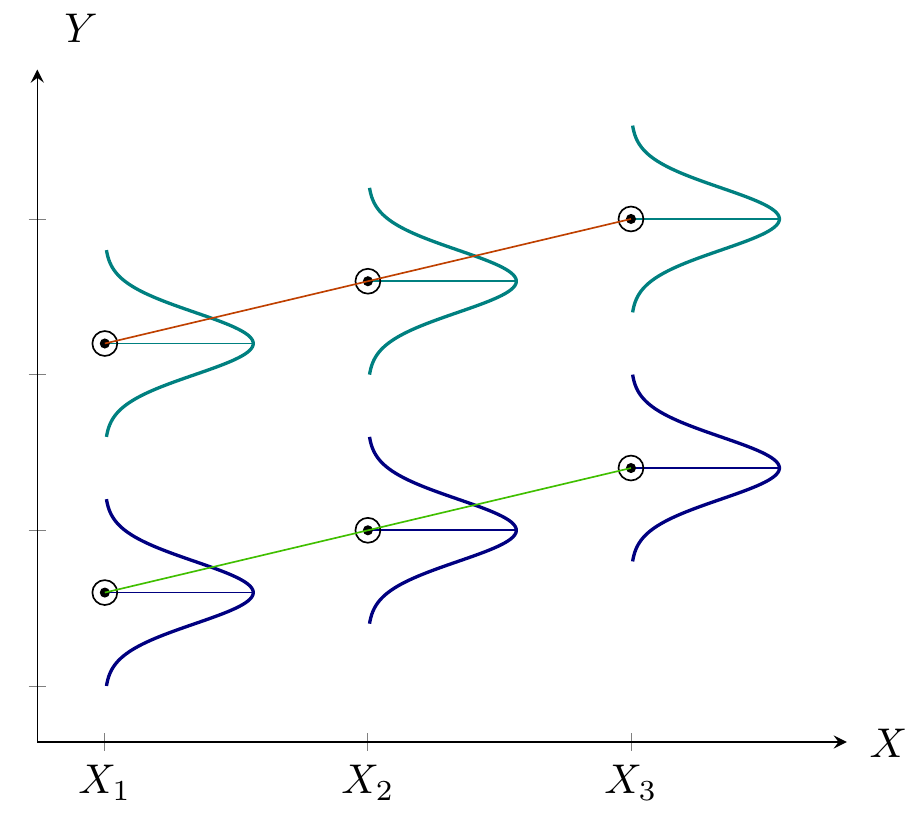
alt text

 

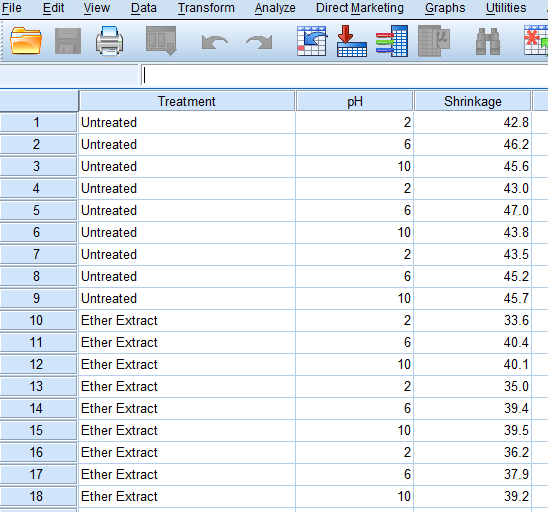
Example

Results of Experiment measuring top shrinkage under 3 treatments (untreated, ether-extracted, ether/alcohol extracted), measured at 3 levels of pH (2, 6, 10) is given in the following table.

Treatment pH Shrinkage
Untreated 2 42.8
Untreated 6 46.2
Untreated 10 45.6
Untreated 2 43.0
Untreated 6 47.0
Untreated 10 43.8
Untreated 2 43.5
Untreated 6 45.2
Untreated 10 45.7
Ether Extract 2 33.6
Ether Extract 6 40.4
Ether Extract 10 40.1
Ether Extract 2 35.0
Ether Extract 6 39.4
Ether Extract 10 39.5
Ether Extract 2 36.2
Ether Extract 6 37.9
Ether Extract 10 39.2
ether/alcohol extracted 2 35.6
ether/alcohol extracted 6 35.2
ether/alcohol extracted 10 36.6
ether/alcohol extracted 2 34.8
ether/alcohol extracted 6 33.0
ether/alcohol extracted 10 32.3
ether/alcohol extracted 2 34.8
ether/alcohol extracted 6 32.3
ether/alcohol extracted 10 35.6

 

Reference

Lindberg, J. (1953). Relationship Between Various Surface Properties of Wool Fibers: Part II: Frictional Properties. Textile Research Journal, 23, 225-237.

 

alt text

 

Same Slopes but different Intercepts

Analyze > General Linear Model > Univariate …

 

alt text
alt text
alt text
alt text
alt text
alt text
alt text

 

Different Intercepts and different Slopes

Analyze > General Linear Model > Univariate …

alt text
alt text
alt text
alt text

 

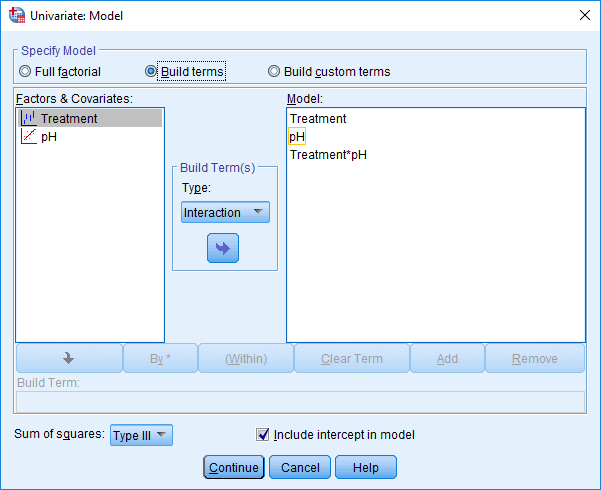
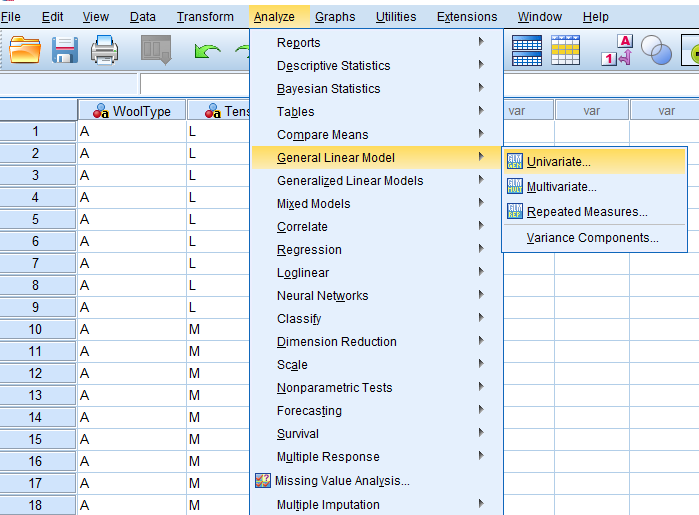
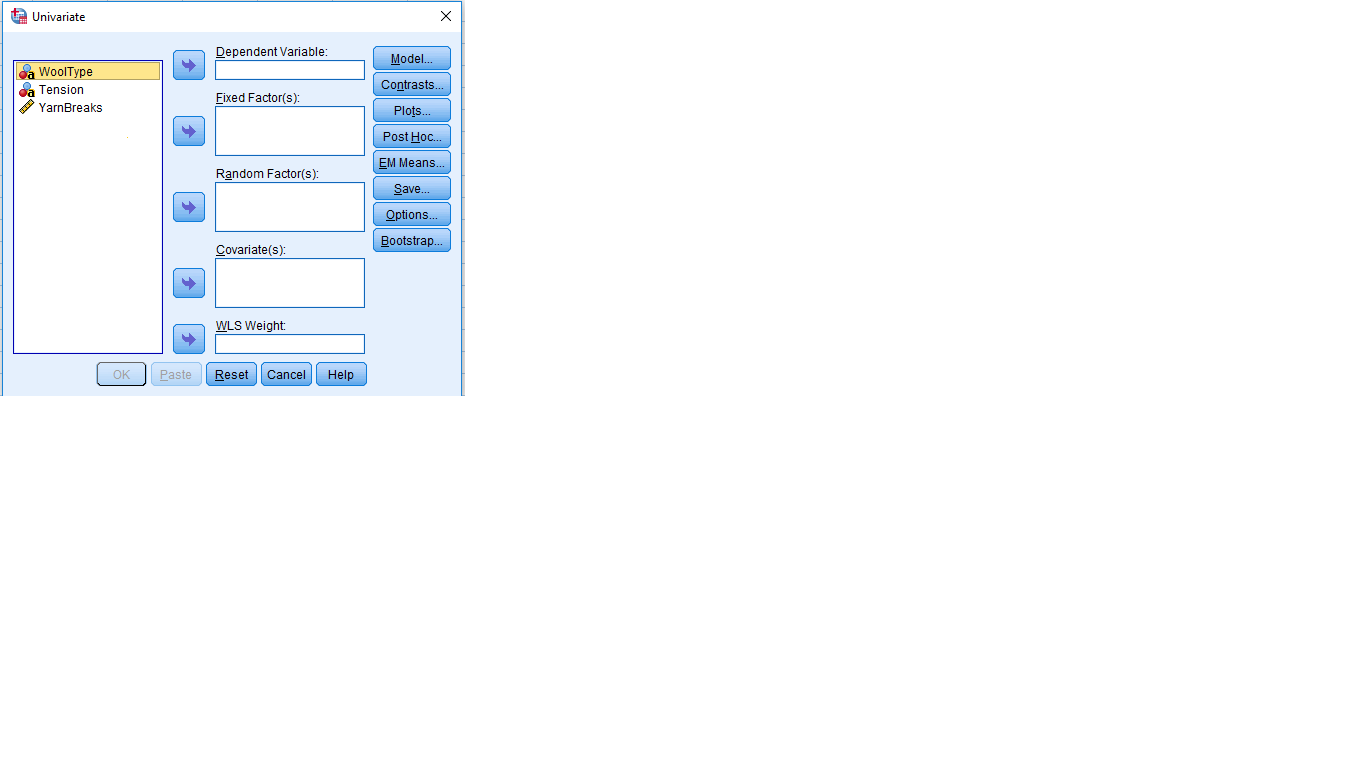
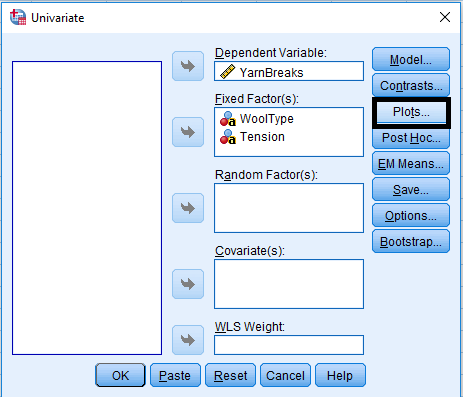
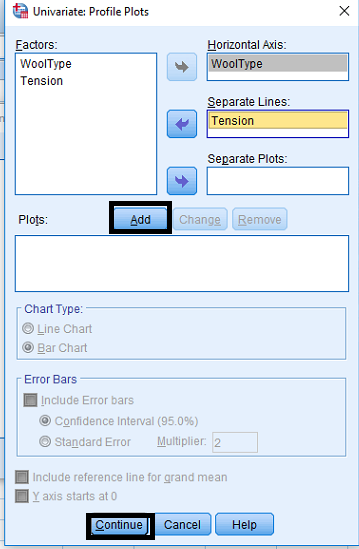
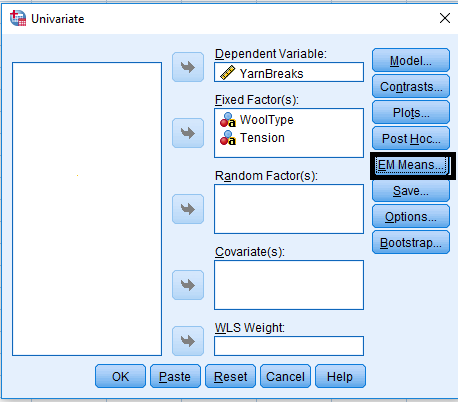
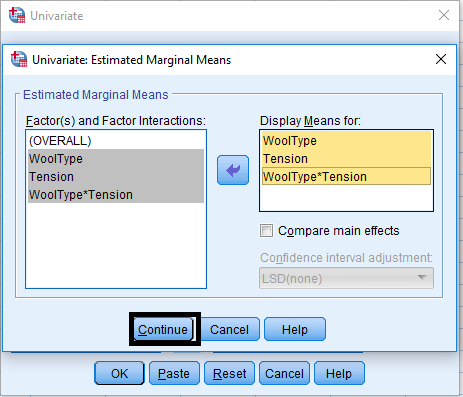
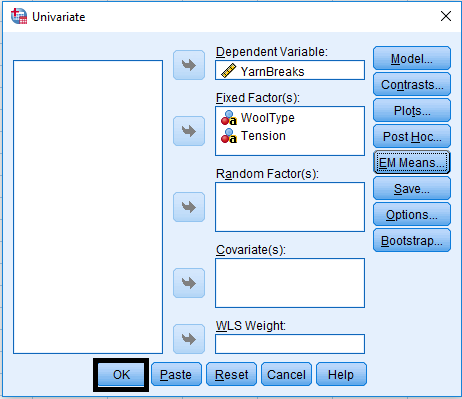
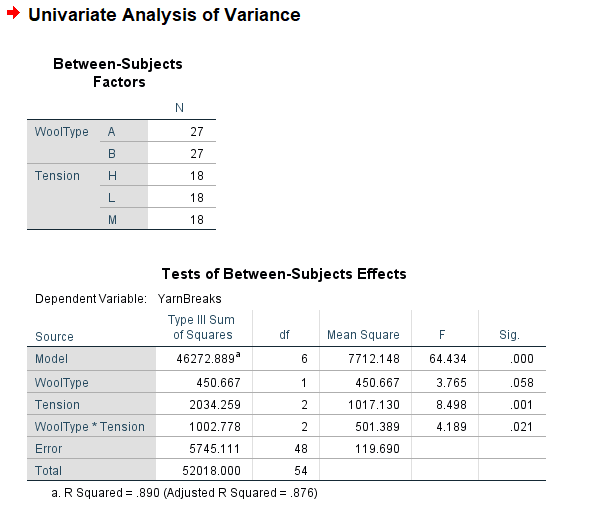
Factorial Experiments

  • Treatments are the combinations of the levels of different factors

 

Example

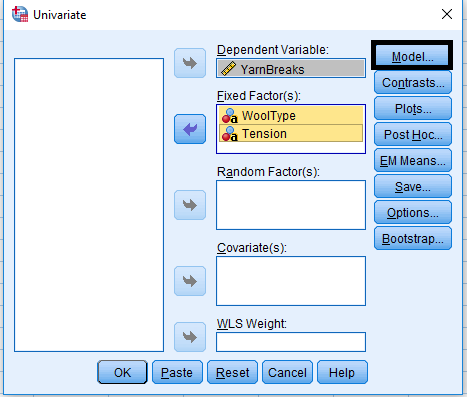
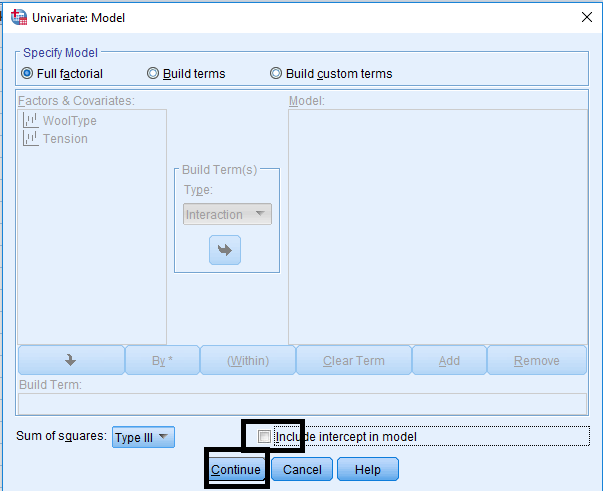
Following data presents the number of warp breaks per loom, where a loom corresponds to a fixed length of yarn for two factors, Wool Type with Two levels (A,B) and Tension with three levels.(Low, Medium, High). Analyze the data with interaction.

WoolType Tension Yarn Breaks
A L 26
A L 30
A L 54
A L 25
A L 70
A L 52
A L 51
A L 26
A L 67
A M 18
A M 21
A M 29
A M 17
A M 12
A M 18
A M 35
A M 30
A M 36
A H 36
A H 21
A H 24
A H 18
A H 10
A H 43
A H 28
A H 15
A H 26
B L 27
B L 14
B L 29
B L 19
B L 29
B L 31
B L 41
B L 20
B L 44
B M 42
B M 26
B M 19
B M 16
B M 39
B M 28
B M 21
B M 39
B M 29
B H 20
B H 21
B H 24
B H 17
B H 13
B H 15
B H 15
B H 16
B H 28

 

Reference

Tippett, L. H. C. (1950). Technological Applications of Statistics. John Wiley & Sons, New York, USA.

 

alt text

 

Analyze > General Linear Model > Univariate …

 

alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text
alt text
All posts by date
comments powered by Disqus