\(\color{green}{\textit{Statistics:}}\) \(\color{green}{\textit{The Art & Science of}}\) \(\color{green}{\textit{Learning from Data}}\)

\(\color{green}{\textit{Muhammad Yaseen}}\)

\(\color{green}{\textit{}}\)

Introduction

Introduction

   

\(\color{green}{\textit{In God we trust,}}\) \(\color{green}{\textit{all others must bring data.}}\)

Introduction

  • \(\color{green}{\textit{In God we trust, all others must bring data.}}\)
    (\(\color{black}{\textit{William E. Deming}}\))

   

  • \(\color{green}{\textit{Statistical thinking will one day be as necessary a}}\) \(\color{green}{\textit{qualification for efficient citizenship as the ability}}\) \(\color{green}{\textit{to read & write.}}\)
    (\(\color{black}{\textit{H.G. Wells}}\))

Introduction

  • \(\color{green}{\textit{To call in the statistician after the experiment is}}\) \(\color{green}{\textit{done may be no more than asking him to perform}}\) \(\color{green}{\textit{a postmortem examination: he may be able to say}}\) \(\color{green}{\textit{what the experiment died of.}}\)
    (\(\color{black}{\textit{R. A. Fisher}}\))

  • \(\color{green}{\textit{If all you have is a hammer, everything looks like}}\) \(\color{green}{\textit{a nail.}}\)
    (\(\color{black}{\textit{Abraham Maslow}}\))

Introduction

Introduction

Introduction

Introduction

Introduction

Decision Review System

Medical Laboratory Test

Karachi Stock Exchange

Heavy Rain in Lahore

Flood in Pakistan 2010

Drought in Pakistan

Wheat Crop in Pakistan

Introduction

  • \(\color{red}{\text{Mathematics}}\) is the \(\color{red}{\text{language}}\) of \(\color{red}{\text{Science}}\)

    • \(2 + 2 = 4\)
    • \(0^{\circ}C = 32^{\circ}F\) (\(\color{blue}{\text{Paradox}}\))
    • Every action has reaction of same extent but opposite direction. (\(\color{blue}{\text{Newton's Third Law}}\))

  • \(\color{green}{\text{Statistics}}\) is the science of \(\color{green}{\text{uncertainty}}\) and \(\color{green}{\text{variability}}\)

  • \(\color{green}{\text{Statistics}}\) is the \(\color{green}{\text{interpretation}}\) of \(\color{green}{\text{Science}}\)

    • \(\color{green}{\text{D}}\)ata \(\color{green}{\text{D}}\)riven \(\color{green}{\text{D}}\)ecisions (\(\color{green}{\text{3Ds}}\))

Reasoning

  • \(\color{green}{\text{Deduction:}}\)

    • Reasoning from \(\color{green}{\text{general}}\) to \(\color{green}{\text{particular}}\).

    • Man is mortal. → Every human being is mortal.

 

  • \(\color{red}{\text{Induction:}}\)
    • Reasoning from \(\color{red}{\text{particular}}\) to \(\color{red}{\text{general}}\).

Statistical Reasoning & Analysis

  • \(\color{green}{\text{Statistics}}\) is the \(\color{green}{\text{science}}\) of \(\color{green}{\text{uncertainty}}\) & \(\color{green}{\text{variability}}\)

 

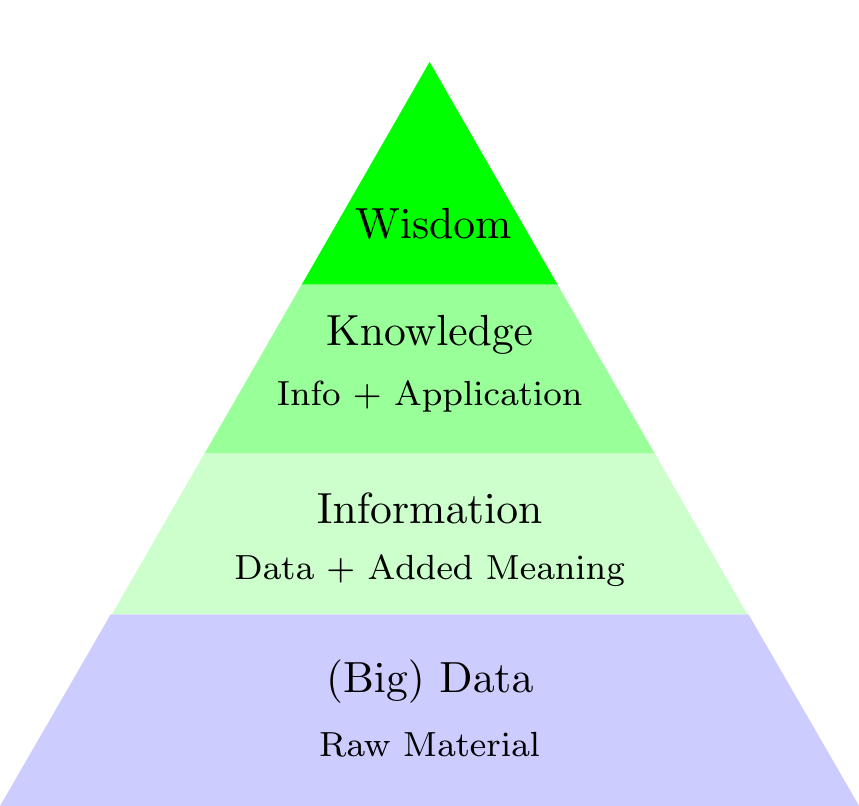
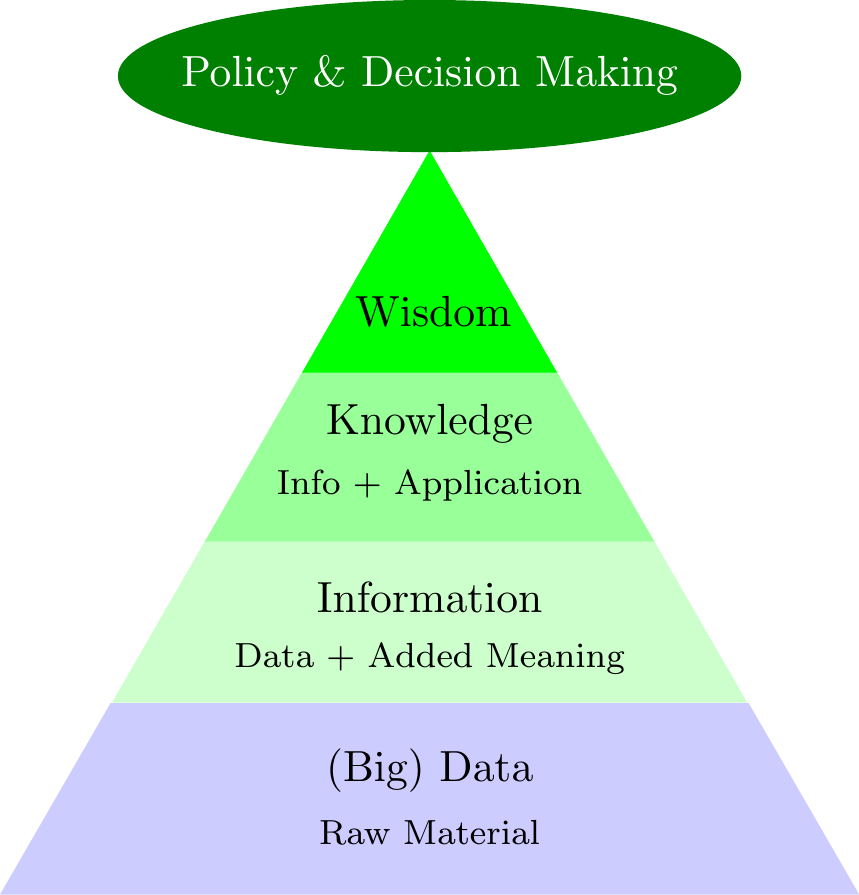
  • Turning \(\color{green}{\text{Data}}\) into \(\color{green}{\text{Information}}\)

    • \(\color{green}{\text{Data}}\) → \(\color{green}{\text{Information}}\) → \(\color{green}{\text{Knowledge}}\) → \(\color{green}{\text{Wisdom}}\)

 

  • \(\color{green}{\text{Statistics}}\) is the \(\color{green}{\text{Art}}\) and \(\color{green}{\text{Science}}\) of \(\color{green}{\text{learning}}\) from \(\color{green}{\text{Data}}\).

Variable

Variable

  • \(\color{red}{\text{Variable:}}\) A \(\color{green}{\text{characteristic}}\) that may \(\color{green}{\text{vary}}\) from \(\color{green}{\text{subject}}\) to \(\color{green}{\text{subject}}\)

  • \(\color{red}{\text{Variables}}\) are \(\color{green}{\text{denoted}}\) by \(\color{green}{\text{last}}\) \(\color{green}{\text{English}}\) \(\color{green}{\text{alphabets}}\) in \(\color{green}{\text{upper}}\) \(\color{green}{\text{case}}\)

  • \(\color{green}{\text{Different observations}}\) of a \(\color{red}{\text{variable}}\) are \(\color{green}{\text{characterized}}\) by \(\color{green}{\text{subscripts}}\)

Measurement & Measurement Scales

Measurement & Measurement Scales

Traffic Signal

Measurement & Measurement Scales

  • \(\color{green}{\text{Measurement}}\)
    • The process of assigning numbers or labels to objects or states in accordance with specific logically accepted rules.

   

  • \(\color{green}{\text{Measurement Scales}}\)
    • Data can be classified according to levels of measurement.
    • The level of measurement of the data often dictates the calculations that can be done to summarize and present the data.
    • It will also determine the statistical tests that should be performed.

Measurement & Measurement Scales

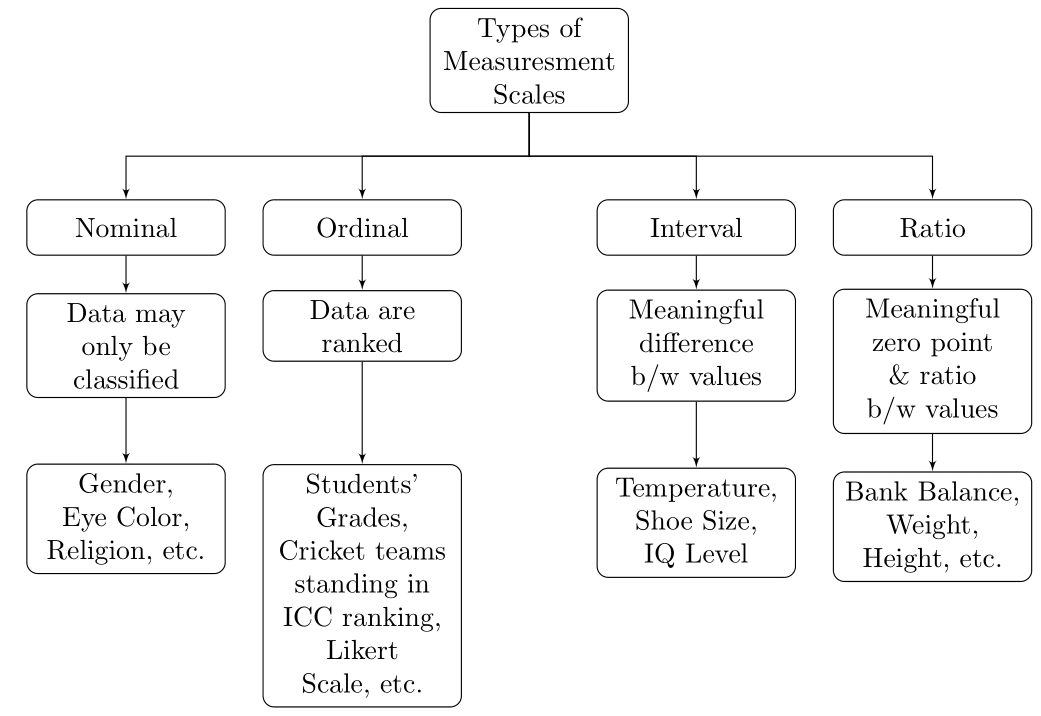
Measurement Scales

Types of Variables

Qualitative & Quantitative Variables

  • \(\color{green}{\text{Qualitative}}\)
    • Nominal or Ordinal variables
  • \(\color{green}{\text{Quantitative}}\)
    • Interval or Ratio variables
      • Discrete
      • Continuous
        • Normal
        • Non-Normal

Dependent & Independent Variables

  • \(\color{green}{\text{Dependent Variable}}\)
    • Variable influenced by other variable(s)

   

  • \(\color{green}{\text{Independent Variable}}\)
    • Variable influencing other variable(s)

Relationship b/w Variables

Dependent & Independent Variables

  • \(\color{green}{\text{Expenditures & Income}}\)
    • Expenditures are influenced by Income.
      • \(\color{green}{\text{Dependent Variable:}}\) Expenditures
      • \(\color{green}{\text{Independent Variable:}}\) Income
        • Expenditures ← Income

 

  • \(\color{green}{\text{CGPA & Study Hours}}\)
    • CGPA is influenced by Study Hours.
      • \(\color{green}{\text{Dependent Variable:}}\) CGPA
      • \(\color{green}{\text{Independent Variable:}}\) Study Hours
        • CGPA ← Study Hours

Dependent & Independent Variables

  • \(\color{green}{\text{Landline Phone Bill & Number of Calls}}\)
    • Landline Phone Bill is affected by Number of Calls made.
      • \(\color{green}{\text{Dependent Variable:}}\) Landline Phone Bill
      • \(\color{green}{\text{Independent Variable:}}\) No. of Calls
        • Bill ← No. of Calls

 

  • \(\color{green}{\text{Crop Production & Amount of Fertilizer}}\)
    • Crop Production is influenced by Amount of Fertilizer used.
      • \(\color{green}{\text{Dependent Variable:}}\) Crop Production
      • \(\color{green}{\text{Independent Variable:}}\) Amount of Fertilizer
        • Crop Production ← Amount of Fertilizer

Types of Relationship

Mathematical Relationship

  • \(\color{green}{\text{Mathematical Relationship}}\)
    • \(\color{red}{\text{Exact Relationship}}\)
    • \(Y = f\left(X\right)\)
    • \(Y \mathrel{\color{red}\leftarrow} X\)

Mathematical Relationship

  • \(\color{green}{\text{Relationship between Area and Radius of a Circle}}\)
    • \(A = f\left(r\right)\)
    • \(A = \pi r^{2}\)
    • \(A \mathrel{\color{red}\leftarrow} r\)

   

  • \(\color{green}{\text{Relationship between Landline Phone Bill and Number of Calls made}}\)
    • \(\text{Bill} = f\left(\text{No. of Calls}\right)\)
    • \(\text{Bill} \mathrel{\color{red}\leftarrow} \text{No. of Calls}\)

Statistical Relationship

  • \(\color{green}{\text{Statistical Relationship}}\)
    • \(\color{red}{\text{Inexact or Probabilistic Relationship}}\)
    • \(Y = f\left(X\right)+\epsilon\)
    • \(Y \mathrel{\color{red}\leftarrow} X\)

Statistical Relationship

  • \(\color{green}{\text{Relationship between Expenditures and Income}}\)
    • \(\text{Expenditures} = f\left(\text{Income}\right)+\epsilon\)
    • \(\text{Expenditures} \mathrel{\color{red}\leftarrow} \text{Income}\)

   

  • \(\color{green}{\text{Relationship between CGPA and Study Hours}}\)
    • \(\text{CGPA} = f\left(\text{Study Hours}\right)+\epsilon\)
    • \(\text{CGPA} \mathrel{\color{red}\leftarrow} \text{Study Hours}\)

Statistical Models

Models

   

\(\color{green}{\textit{All models are wrong,}}\) \(\color{green}{\textit{but some are useful.}}\)

Linear Model

 

  • \(\color{green}{\text{Expenditures & Income}}\)
    • \(\color{green}{\text{Expenditures are influenced by Income}}\)
    • \(\text{Expenditures} \mathrel{\color{red}\leftarrow} \text{Income}\)
  • \(\color{green}{\text{Expenditures & Gender}}\)
    • \(\color{green}{\text{Expenditures are influenced by Gender}}\)
    • \(\text{Expenditures} \mathrel{\color{red}\leftarrow} \text{Gender}\)
  • \(\color{green}{\text{Expenditures, Income & Gender}}\)
    • \(\color{green}{\text{Expenditures are influenced by Income & Gender}}\)
    • \(\text{Expenditures} \mathrel{\color{red}\leftarrow} \text{Income} + \text{Gender}\)

Linear Model

 

  • \(\color{green}{\text{CGPA & Study Hours}}\)
    • \(\color{green}{\text{CGPA is influenced by Study Hours}}\)
    • \(\text{CGPA} \mathrel{\color{red}\leftarrow} \text{Study Hours}\)
  • \(\color{green}{\text{CGPA & Gender}}\)
    • \(\color{green}{\text{CGPA is influenced by Gender}}\)
    • \(\text{CGPA} \mathrel{\color{red}\leftarrow} \text{Gender}\)
  • \(\color{green}{\text{CGPA, Study Hours & Gender}}\)
    • \(\color{green}{\text{CGPA is influenced by Study Hours & Gender}}\)
    • \(\text{CGPA} \mathrel{\color{red}\leftarrow} \text{Study Hours} + \text{Gender}\)

Linear Model

 

  • \(\color{green}{\text{Weight Gain & Intake}}\)
    • \(\color{green}{\text{Weight Gain is influenced by Intake}}\)
    • \(\text{Weight Gain} \mathrel{\color{red}\leftarrow} \text{Intake}\)
  • \(\color{green}{\text{Weight Gain & Feed Type}}\)
    • \(\color{green}{\text{Weight Gain is influenced by Feed Type}}\)
    • \(\text{Weight Gain} \mathrel{\color{red}\leftarrow} \text{Feed Type}\)
  • \(\color{green}{\text{Weight Gain, Intake & Feed Type}}\)
    • \(\color{green}{\text{Weight Gain is influenced by Intake & Feed Type}}\)
    • \(\text{Weight Gain} \mathrel{\color{red}\leftarrow} \text{Intake} + \text{Feed Type}\)

Linear Model

 

  • \(\color{green}{\text{Yield & Amount of Fertilizer}}\)
    • \(\color{green}{\text{Yield of a crop is influenced by Amount of Fertilizer}}\)
    • \(\text{Yield} \mathrel{\color{red}\leftarrow} \text{Amount of Fertilizer}\)
  • \(\color{green}{\text{Yield & Varieties}}\)
    • \(\color{green}{\text{Yield of a crop is influenced by Varieties}}\)
    • \(\text{Yield} \mathrel{\color{red}\leftarrow} \text{Varieties}\)
  • \(\color{green}{\text{Yield Amount of Fertilizer & Varieties}}\)
    • \(\color{green}{\text{Yield of a crop is influenced by Amount of Fertilizer & Varieties}}\)
    • \(\text{Yield} \mathrel{\color{red}\leftarrow} \text{Amount of Fertilizer} + \text{Varieties}\)

Regression Model

Regression Model

   

  • \(\color{green}{\text{Quantify the dependency of a Normal variable on}}\) \(\color{green}{\text{one or more quantitative variable(s)}}\)

Regression Model

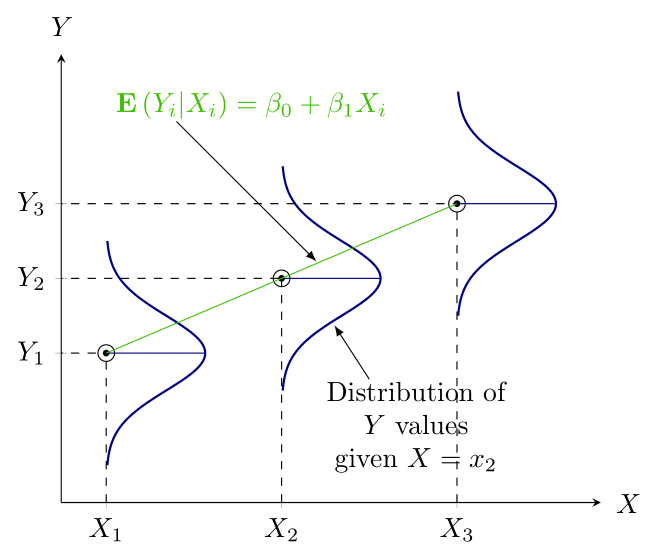
Population Regression Function

ANOVA Model

ANOVA Model

 

  • \(\color{green}{\text{Comparing means of Normal dependent variable}}\) \(\color{green}{\text{for levels of different factors}}\)

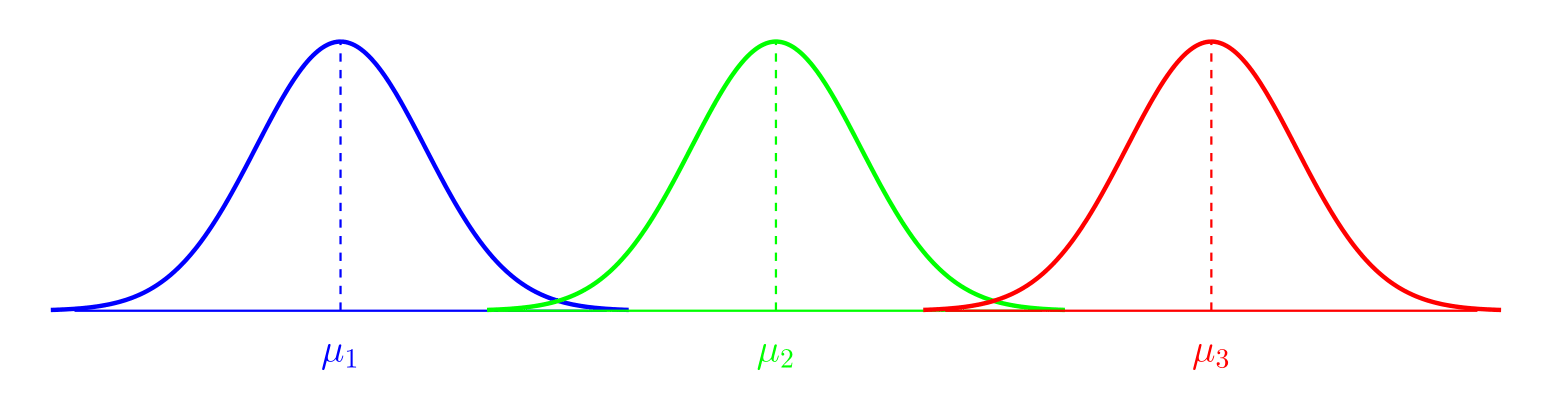
ANOVA Model

ANCOVA Model

ANCOVA Model

   

  • \(\color{green}{\text{Quantify the dependency of a Normal variable on}}\) \(\color{green}{\text{one or more quantitative variable(s)}}\)

   

  • \(\color{green}{\text{Comparing means of Normal dependent variable}}\) \(\color{green}{\text{for levels of different factors}}\)

ANCOVA Model

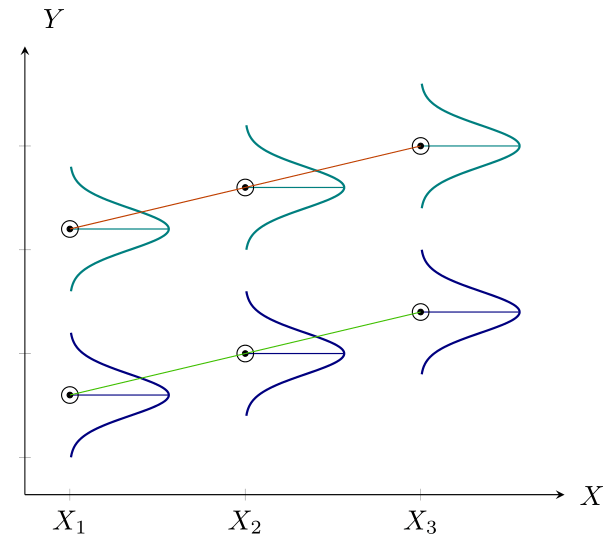
ANCOVA Model

Treatment Structure

Treatment Structure

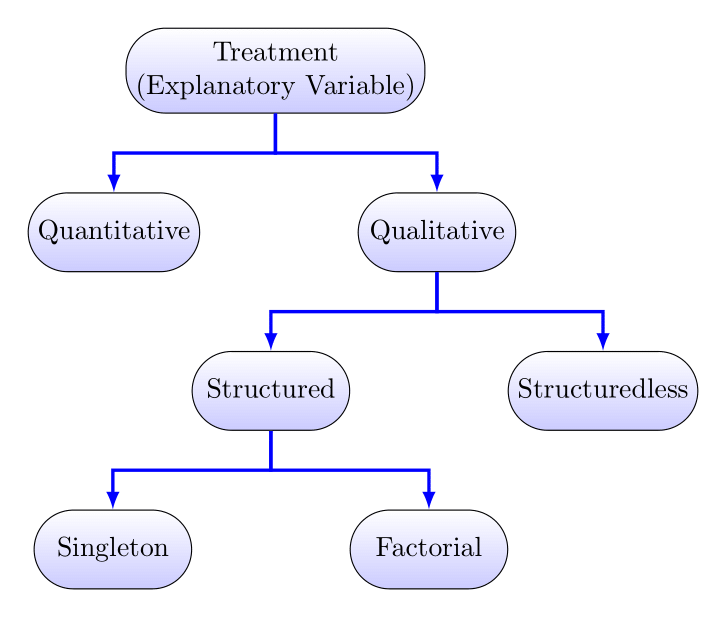
Treatment Structure

Treatment Structure

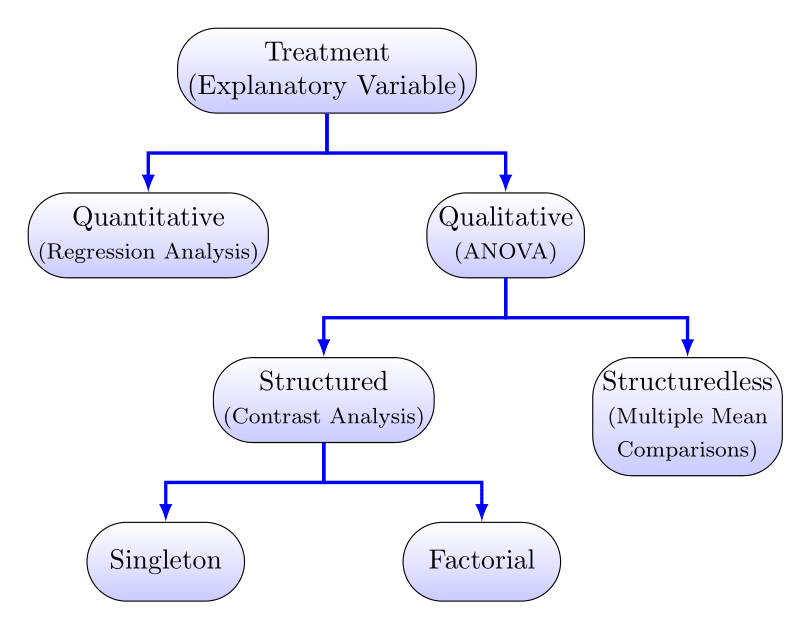
Treatment Structure

References

Fox, J. (2015). Applied Regression Analysis & Generalized Linear Models. SAGE Publications, Inc.

McCulloch, C. E., S. R. Searle, and J. M. Neuhaus (2008). Generalized, Linear, & Mixed Models. John Wiley & Sons.

Pezzullo, J. C. (2018). Biostatistics for Dummies. John Wiley & Sons, Inc.

R Core Team (2022). R: A Language & Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna, Austria. URL: http://www.R-project.org/.

References (Cont’d…)

Searle, S. R. and M. H. J. Gruber (2016). Linear Models. John Wiley & Sons.

Sullivan, L. M. (2018). Essentials of Biostatistics in Public Health. Jones & Bartlett Learning.

Triola, M. F. (2018). Elementary Statistics. Pearson Education, Inc.

Triola, M. M., M. F. Triola, and J. Roy (2018). Biostatistics for the Biological & Health Sciences. Pearson Education, Inc.

\(\color{green}{\textit{Muhammad Yaseen, PhD (Statistics, UNL-USA)}}\), https://myaseen208.com